在 R 中估计 GARCH 参数存在的问题（续）

本文承接《在 R 中估计 GARCH 参数存在的问题》

链接：https://www.cnblogs.com/xuruilong100/p/9986088.html

在之前的博客《在 R 中估计 GARCH 参数存在的问题》中，Curtis Miller 讨论了 fGarch 包和 tseries 包估计 GARCH(1, 1) 模型参数的稳定性问题，结果不容乐观。本文承接之前的博客，继续讨论估计参数的稳定性，这次使用的是前文中提到，但没有详尽测试的 rugarch 包。

`rugarch` 包的使用

rugarch 包中负责估计 GARCH 模型参数的最主要函数是 ugarchfit，不过在调用该函数值前要用函数 ugarchspec 创建一个特殊对象，用来固定 GARCH 模型的阶数。

srs = ...
garch_mod = ugarchspec(
    variance.model = list(
        garchOrder = c(1, 1)),
    mean.model = list(
        armaOrder = c(0, 0),
        include.mean = FALSE))
g <- ugarchfit(spec = garch_mod, data = srs)

需要注意的是 g 是一个 S4 类。

简单实验

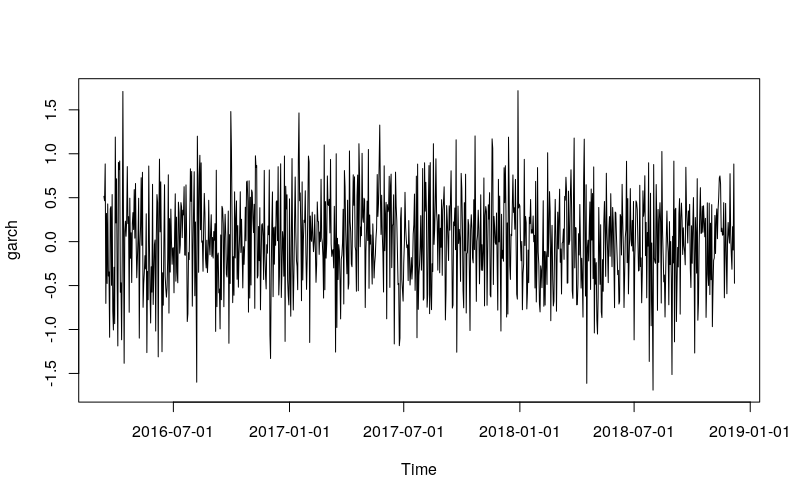
首先用 1000 个模拟样本，

library(rugarch)
library(ggplot2)
library(fGarch)
set.seed(110117)
x <- garchSim(
    garchSpec(
        model = list(
            "alpha" = 0.2, "beta" = 0.2, "omega" = 0.2)),
    n.start = 1000,
    n = 1000)
plot(x)

garch_spec = ugarchspec(
    variance.model = list(garchOrder = c(1, 1)),
    mean.model = list(
        armaOrder = c(0, 0), include.mean = FALSE))
g_all <- ugarchfit(
    spec = garch_spec, data = x)
g_50p <- ugarchfit(
    spec = garch_spec, data = x[1:500])
g_20p <- ugarchfit(
    spec = garch_spec, data = x[1:200])

结果同样不容乐观，

coef(g_all)
#        omega       alpha1        beta1 
# 2.473776e-04 9.738059e-05 9.989026e-01
coef(g_50p)
#        omega       alpha1        beta1 
# 2.312677e-04 4.453120e-10 9.989998e-01 
coef(g_20p)
#      omega     alpha1      beta1 
# 0.03370291 0.09823614 0.79988068

再用 10000 个模拟样本试试，如果使用日线级别的数据的话，这相当于 40 年长度的数据量，

set.seed(110117)
x <- garchSim(
    garchSpec(
        model = list(
            "alpha" = 0.2, "beta" = 0.2, "omega" = 0.2)),
    n.start = 1000, n = 10000)
plot(x)
g_all <- ugarchfit(
    spec = garch_spec, data = x)
g_50p <- ugarchfit(
    spec = garch_spec, data = x[1:5000])
g_20p <- ugarchfit(
    spec = garch_spec, data = x[1:2000])

coef(g_all)
#     omega    alpha1     beta1 
# 0.1955762 0.1924522 0.1967614 
coef(g_50p)
#     omega    alpha1     beta1 
# 0.2003755 0.1919633 0.1650453
coef(g_20p)
#        omega       alpha1        beta1 
# 1.368689e-03 6.757177e-09 9.951920e-01

看来数据量极端大的时候，估计才可能是合理的、稳定的。

rugarch 参数估计的行为

首先使用 1000 个模拟样本做连续估计，样本数从 500 升至 1000。

library(doParallel)
cl <- makeCluster(detectCores() - 1)
registerDoParallel(cl)
set.seed(110117)
x <- garchSim(
    garchSpec(
        model = list(alpha = 0.2, beta = 0.2, omega = 0.2)),
    n.start = 1000, n = 1000)
params <- foreach(
    t = 500:1000,
    .combine = rbind,
    .packages = c("rugarch")) %dopar%
    {
        getFitDataRugarch(x[1:t])
    }
rownames(params) <- 500:1000
params_df <- as.data.frame(params)
params_df$t <- as.numeric(rownames(params))
ggplot(params_df) +
    geom_line(
        aes(x = t, y = beta1)) +
    geom_hline(
        yintercept = 0.2, color = "blue") +
    geom_ribbon(
        aes(x = t,
            ymin = beta1 - 2 * beta1.se,
            ymax = beta1 + 2 * beta1.se),
        color = "grey", alpha = 0.5) +
    ylab(expression(hat(beta))) +
    scale_y_continuous(
        breaks = c(0, 0.2, 0.25, 0.5, 1)) +
    coord_cartesian(ylim = c(0, 1))

几乎所有关于 \(\beta\) 的估计都非常肯定的被认为是 1！这个结果相较于 fGarch 包来说，更加糟糕。

让我们看看其他参数的行为。

library(reshape2)
library(plyr)
library(dplyr)
param_reshape <- function(p)
{
    p <- as.data.frame(p)
    p$t <- as.integer(rownames(p))
    pnew <- melt(p, id.vars = "t", variable.name = "parameter")
    pnew$parameter <- as.character(pnew$parameter)
    pnew.se <- pnew[grepl("*.se", pnew$parameter), ]
    pnew.se$parameter <- sub(".se", "", pnew.se$parameter)
    names(pnew.se)[3] <- "se"
    pnew <- pnew[!grepl("*.se", pnew$parameter), ]
    return(
        join(
            pnew, pnew.se,
            by = c("t", "parameter"),
            type = "inner"))
}
ggp <- ggplot(
    param_reshape(params),
    aes(x = t, y = value)) +
    geom_line() +
    geom_ribbon(
        aes(ymin = value - 2 * se,
            ymax = value + 2 * se),
        color = "grey",
        alpha = 0.5) +
    geom_hline(yintercept = 0.2, color = "blue") +
    scale_y_continuous(
        breaks = c(0, 0.2, 0.25, 0.5, 0.75, 1)) +
    coord_cartesian(ylim = c(0, 1)) +
    facet_grid(. ~ parameter)
print(ggp + ggtitle("solnp Optimization"))

这种现象不仅限于 \(\beta\)，\(\omega\) 和 \(\alpha\) 也表现出极端不良行为。

极端大样本

下面将样本总数扩充至 10000，连续估计的样本数从 5000 升至 10000，情况有会怎么样？

set.seed(110117)
x <- garchSim(
    garchSpec(
        model = list(alpha = 0.2, beta = 0.2, omega = 0.2)),
    n.start = 1000, n = 10000)
params10k <- foreach(
    t = seq(5000, 10000, 100),
    .combine = rbind,
    .packages = c("rugarch")) %dopar%
    {
        getFitDataRugarch(x[1:t])
    }
rownames(params10k) <- seq(5000, 10000, 100)
params10k_df <- as.data.frame(params10k)
params10k_df$t <- as.numeric(rownames(params10k))
ggplot(params10k_df) +
    geom_line(
        aes(x = t, y = beta1)) +
    geom_hline(
        yintercept = 0.2, color = "blue") +
    geom_ribbon(
        aes(x = t,
            ymin = beta1 - 2 * beta1.se,
            ymax = beta1 + 2 * beta1.se),
        color = "grey", alpha = 0.5) +
    ylab(expression(hat(beta))) +
    scale_y_continuous(
        breaks = c(0, 0.2, 0.25, 0.5, 1)) +
    coord_cartesian(ylim = c(0, 1))

结果堪称完美！之前的猜测是对的，样本要极端大才能保证估计的质量。

其他参数的行为。

ggp10k <- ggplot(
    param_reshape(params10k),
    aes(x = t, y = value)) +
    geom_line() +
    geom_ribbon(
        aes(ymin = value - 2 * se,
            ymax = value + 2 * se),
        color = "grey",
        alpha = 0.5) +
    geom_hline(yintercept = 0.2, color = "blue") +
    scale_y_continuous(
        breaks = c(0, 0.2, 0.25, 0.5, 0.75, 1)) +
    coord_cartesian(ylim = c(0, 1)) +
    facet_grid(. ~ parameter)
print(ggp10k + ggtitle("solnp Optimization"))