[labuladong算法小抄]如何k个一组反转链表

来源：cnblogs　　作者：陶士涵　　时间：2021/1/18 16:29:45　　对本文有异议

摘自labuladong算法小抄，使用go语言重新描述

之前的文章「递归反转链表的一部分」讲了如何递归地反转一部分链表，有读者就问如何迭代地反转链表，这篇文章解决的问题也需要反转链表的函数，我们不妨就用迭代方式来解决。

本文要解决「K 个一组反转链表」，不难理解：

这个问题经常在面经中看到，而且 LeetCode 上难度是 Hard，它真的有那么难吗？

对于基本数据结构的算法问题其实都不难，只要结合特点一点点拆解分析，一般都没啥难点。下面我们就来拆解一下这个问题。

一、分析问题

首先，前文学习数据结构的框架思维提到过，链表是一种兼具递归和迭代性质的数据结构，认真思考一下可以发现这个问题具有递归性质。

什么叫递归性质？直接上图理解，比如说我们对这个链表调用 reverseKGroup(head, 2)，即以 2 个节点为一组反转链表：

如果我设法把前 2 个节点反转，那么后面的那些节点怎么处理？后面的这些节点也是一条链表，而且规模（长度）比原来这条链表小，这就叫子问题。

我们可以直接递归调用 reverseKGroup(cur, 2)，因为子问题和原问题的结构完全相同，这就是所谓的递归性质。

发现了递归性质，就可以得到大致的算法流程：

1、先反转以 head 开头的 k 个元素。

2、将第 k + 1 个元素作为 head 递归调用 reverseKGroup 函数。

3、将上述两个过程的结果连接起来。

整体思路就是这样了，最后一点值得注意的是，递归函数都有个 base case，对于这个问题是什么呢？

题目说了，如果最后的元素不足 k 个，就保持不变。这就是 base case，待会会在代码里体现。

二、代码实现

首先，我们要实现一个 ReverseSingleList 函数反转一个区间之内的元素。在此之前我们再简化一下，给定链表头结点，如何反转整个链表？

// 反转以 a 为头结点的链表
func ReverseSingleList(a *ListNode) *ListNode {
    var (
        pre, cur, nxt *ListNode
    )
    pre = nil
    cur = a
    nxt = a
    for cur != nil {
        nxt = cur.next
        // 逐个结点反转
        cur.next = pre
        // 更新指针位置
        pre = cur
        cur = nxt
    }
    // 返回反转后的头结点
    return pre
}

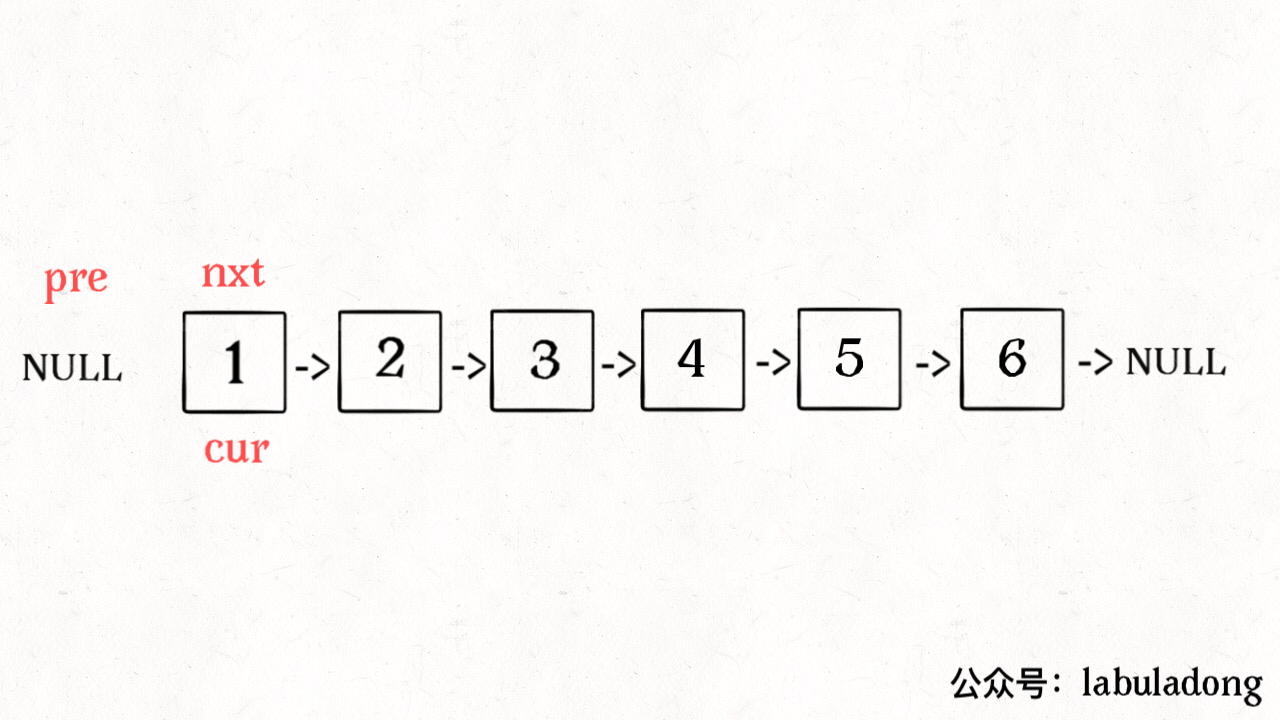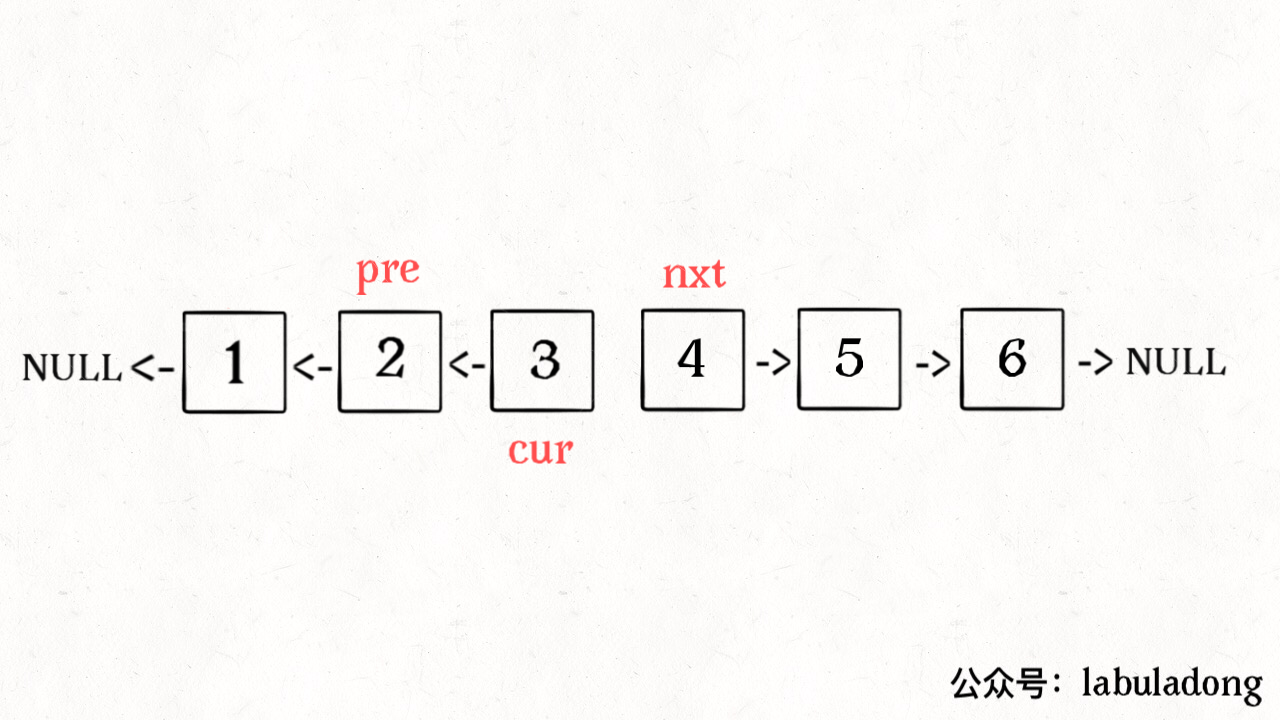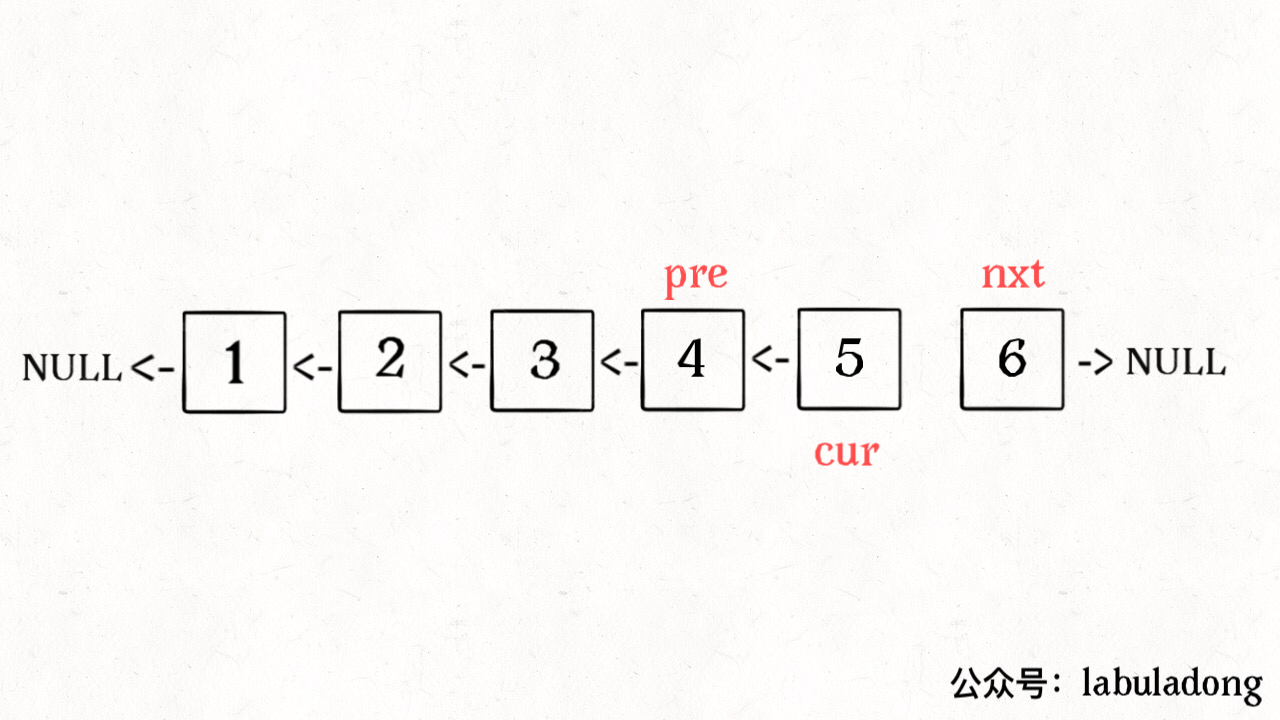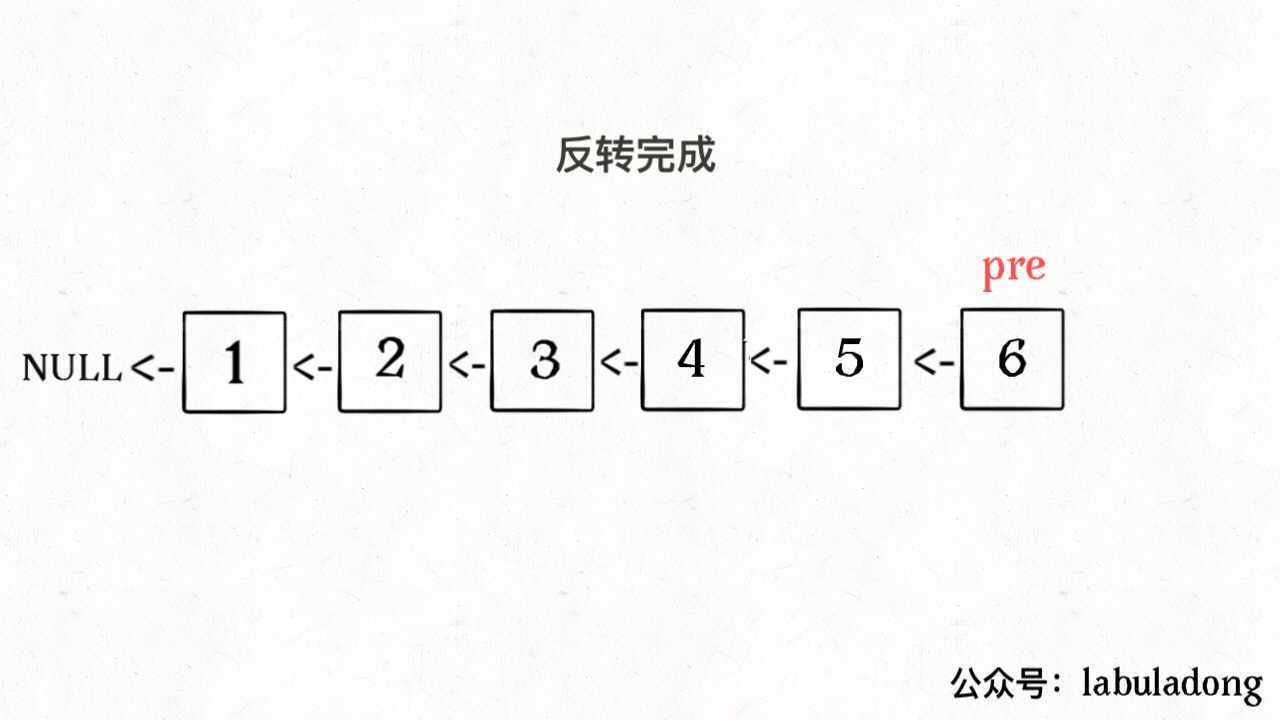
这次使用迭代思路来实现的，借助动画理解应该很容易。

「反转以 a 为头结点的链表」其实就是「反转 a 到 null 之间的结点」，那么如果让你「反转 a 到 b 之间的结点」，你会不会？

只要更改函数签名，并把上面的代码中 null 改成 b 即可：

/** 反转区间 [a, b) 的元素，注意是左闭右开 */
func ReverseSingleList(a *ListNode, b *ListNode) *ListNode {
    var (
        pre, cur, nxt *ListNode
    )
    pre = nil
    cur = a
    nxt = a
    //终止的条件改一下就行了
    for cur != b {
        nxt = cur.next
        // 逐个结点反转
        cur.next = pre
        // 更新指针位置
        pre = cur
        cur = nxt
    }
    // 返回反转后的头结点
    return pre
}

现在我们迭代实现了反转部分链表的功能，接下来就按照之前的逻辑编写 reverseKGroup 函数即可：

func ReverseKGroup(head *ListNode, k int) *ListNode {
    if head == nil {
        return nil
    }
    // 区间 [a, b) 包含 k 个待反转元素
    var (
        a, b *ListNode
    )
    b = head
    a = head
    for i := 0; i < k; i++ {
        // 不足 k 个，不需要反转，base case
        if b == nil {
            return head
        }
        b = b.next
    }
    // 反转前 k 个元素
    newHead := ReverseSingleList(a, b)
    // 递归反转后续链表并连接起来
    a.next = ReverseKGroup(b, k)
    return newHead
}