树形DP 保卫王国P5024
前置知识
1、邻接表 + Dfs(深度优先搜索)
2、基础DP(如 01背包 )
3、最小公共祖先(LCA)
首先解读一下题意
城市即为节点
每个节点都有一个驻军资金 即节点的权值
现在要让每两个节点之间至少有一个节点拥有驻军
并给出 m 个要求
求出每个要求所对应的最小花费
为了更好的阅读体验
- 三个方法的完整代码将放在文章最后
- 请先大致浏览完完整代码再阅读解释
- 请配合草稿本画图并记录变量名含义
无优化 44分
解题方法
树形DP
顾名思义 是在树形结构中使用动态规划
DP是一种暴力算法
因此把每个节点取与不取的子树最小权值都算出来
就可在根上算出答案
算法评估
由于有多个要求
因此有几个要求 dfs就会执行几次
这导致运行时间大大变长
由于44分代码比较简单 所以就直接把注释打入代码了
部分优化 68分
解题方法
现在我们要想办法解决重复执行的问题
我们可以通过一个预处理来把他们之间之外的算出来
这样就可以大大提升运算速度

下半部分的红色我们已经搞定了
就和无优化部分的一样 处理出 \(f[i][0/1]\) 即可
而对于 \(ff[i][0/1]\) 就要用从上往下的Dfs来解决了 具体看代码
求ff
void dfs2(int u,int fa){ for(int i = head[u];i;i = e[i].u){ int ev = e[i].v; if(ev == fa) continue; ff[ev][0] = ff[u][1] + f[u][1] - min(f[ev][0],f[ev][1]); ff[ev][1] = min(ff[u][0] + f[u][0] - f[ev][1],ff[ev][0]); dfs2(ev,u); }}
主要来看看这两个状态转移方程
\(ff[ev][0]\) :既然ev为0(不可取) 则u必须为1(可取)
\(f[ev][1]\) :ev为0(取) 则u为0/1皆可
所以求出\(ff[ev][0/1]\)通过以上两个方程即可

可以看到Dfs2的调用被放在了状态转移方程的下面
因为这个Dfs是自上而下的 所以在上面处理完后再进行下面的调用
关于trans函数
void trans(int id){ int a = rest[id].node1; int b = rest[id].node2; int x = rest[id].val1; int y = rest[id].val2; memset(dp,sizeof(dp),0); if(x == 0){ dp[a][0] = f[a][0]; dp[a][1] = INF; } else { dp[a][1] = f[a][1]; dp[a][0] = INF; } if(y == 0){ dp[b][0] = f[b][0]; dp[b][1] = INF; } else { dp[b][1] = f[b][1]; dp[b][0] = INF; }}
在无优化中 trans函数是编辑了vis数组
而在部分优化中 trans函数直接将对应的dp值设置为最大值-INF
这样在min中的挑选下,肯定能将设为INF的状态过滤掉
关于LCAans函数
ll LCAans(int x,int y){ int t; if(deep[x] < deep[y]) swap(x,y);//调换x为跟深的节点 while (deep[x] > deep[y] && father[x] != y){//调节至同一深度&&x不为y t = father[x]; dp[t][1] = f[t][1] - min(f[x][0],f[x][1]) + min(dp[x][0],dp[x][1]); dp[t][0] = f[t][0] - f[x][1] + dp[x][1]; x = t; } if(father[x] == y){//若x为y的儿子 dp[y][1] = dp[y][1] - min(f[x][0],f[x][1]) + min(dp[x][0],dp[x][1]); dp[y][0] = dp[y][0] - f[x][1] + dp[x][1]; return min(dp[y][1] + ff[y][1],dp[y][0] + ff[y][0]); } while(father[x] != father[y]){//共同向上 t = father[x]; dp[t][1] = f[t][1] - min(f[x][0],f[x][1]) + min(dp[x][0],dp[x][1]); dp[t][0] = f[t][0] - f[x][1] + dp[x][1]; x = t; t = father[y]; dp[t][1] = f[t][1] - min(f[y][0],f[y][1]) + min(dp[y][0],dp[y][1]); dp[t][0] = f[t][0] - f[y][1] + dp[y][1]; y = t; } t = father[x];//处理LCA节点时等于将两边都砍掉重新接 dp[t][1] = f[t][1] - min(f[x][0],f[x][1]) + min(dp[x][0],dp[x][1]) - min(f[y][0],f[y][1]) + min(dp[y][0],dp[y][1]); dp[t][0] = f[t][0] - f[x][1] + dp[x][1] - f[y][1] + dp[y][1]; return min(dp[t][0] + ff[t][0],dp[t][1] + ff[t][1]);}
这是LCA非倍增的写法
遍历全代码 可以发现基本上都是重复的:
t = father[x/y]; dp[t][1] = f[t][1] - min(f[x/y][0],f[x/y][1]) + min(dp[x/y][0],dp[x/y][1]); dp[t][0] = f[t][0] - f[x/y][1] + dp[x/y][1];
理解性来看
就是把t节点的下半部分置换成更新好的下半部分
然后作为其dp值
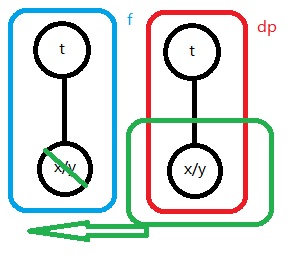
还有一点要强调
就是若x为y的儿子那块
被砍腿的是dp数组而不是f数组
因为y也是有要求的
但是f[y]没有被INF给标记过
因此要用被标记过的dp来砍
main()函数中要注意的几点
//只截取了for循环的部分 trans(i); ll res = LCAans(rest[i].node1,rest[i].node2); if(res < INF) cout << res << endl; else cout << "-1" << endl;
-
记得调用trans(i)
-
LCAans的代入值是node1,node2
-
要加入res与INF的比较
算法评估
通过两次Dfs求出了 \(f\) 和 \(ff\) 数组
将上下两端的计算量大大减少
明显提升的算法效率
但是遇到中间部分比较长的情况
就需要用到大量的时间来反复处理
既然是LCA 那自然可以想到倍增的算法
接下来就进行倍增的处理
百分优化
解题方法
100分代码与68分代码大致相同
共有以下变化
- father增加了对次方祖先的表达
- 用两个一维小数组来代替dp数组
- 添加了LCA函数
father数组
之前的father数组只用于表达节点的亲生父亲
而现在表达的是 u 的 \(2^t\) 辈祖先
因此dfs1中的father的表达也要有所改变:
father[u][0] = fa;
\(2^0 = 1\) 即为 u 的亲生父亲
LCA函数
其主要作用是计算出fa数组 ———用于倍增是树段的计算
fa数组就是这个优化的核心部分
fa数组代表的含义为
u节点的 \(2^t\) 辈祖先为根的子树 减去 u节点为根的子树
所对应的最小权值
第一个0(不取)/1(取)对应u
第二个0(不取)/1(取)对应u的\(2^t\)辈祖先

这个fa数组是用递推求出的:
void LCA(){ for(int i = 1;i <= n;i++){ int t = father[i][0]; fa[i][0][0][0] = INF; fa[i][0][0][1] = f[t][1] - min(f[i][0],f[i][1]); fa[i][0][1][0] = f[t][0] - f[i][1]; fa[i][0][1][1] = fa[i][0][0][1]; } for(int t = 1;t <= 20;t++){ for(int i = 1;i <= n;i++){ int X = father[i][t-1]; father[i][t] = father[X][t-1]; fa[i][t][0][0] = min(fa[i][t-1][0][0] + fa[X][t-1][0][0], fa[i][t-1][0][1] + fa[X][t-1][1][0]); fa[i][t][0][1] = min(fa[i][t-1][0][0] + fa[X][t-1][0][1], fa[i][t-1][0][1] + fa[X][t-1][1][1]); fa[i][t][1][0] = min(fa[i][t-1][1][0] + fa[X][t-1][0][0], fa[i][t-1][1][1] + fa[X][t-1][1][0]); fa[i][t][1][1] = min(fa[i][t-1][1][0] + fa[X][t-1][0][1], fa[i][t-1][1][1] + fa[X][t-1][1][1]); } }}
第一个for循环
这是递推的基础
定义 t 为i的亲生父亲
fa[i][0][0][0]:
i和t都为0(不取) 不符合题意 因此取INF
fa[i][0][0][1]:
i不取t取 因为t是取的 所以f[i]是要取min的
fa[i][0][1][0]:
i取t不取 因为t是不取 所以f[i]只能为1
fa[i][0][1][1]:
i取t取 因为都是自由的 所以和 fa[i][0][0][1] 相同
第二个for循环
原理:
这里用了一个中将量 X
处理 X 的 0/1 状态
因为 fa 是已经处理好的最小权值
所以直接简单相加就可以了
可行性:
t 代表 i 的 \(2^t\) 辈祖先
由于循环外层是 t 内层为 i
说明 t - 1 层已经循环处理完毕了
因此用 X 这个中间量是可以的
father数组:
利用 X 这个中间值可递推出father
可行性与上文相同
LCAans函数
ll LCAans(int x,int y,int val1,int val2){ ll tx[2] = {0,0}; ll ty[2] = {0,0}; dpx[0] = dpx[1] = INF; dpy[0] = dpy[1] = INF; if(deep[x] < deep[y]){ swap(x,y); swap(val1,val2); } dpx[val1] = f[x][val1]; dpy[val2] = f[y][val2];
我们为了实现0/1的要求
我们先把 dpx 和 dpy 全部赋值成 INF
然后再将可通行的赋值为正常值
for(int t = 20;t >= 0;t--){ if((deep[x] - deep[y]) >= (1<<t)){ tx[0] = min(fa[x][t][0][0] + dpx[0], fa[x][t][1][0] + dpx[1]); tx[1] = min(fa[x][t][0][1] + dpx[0], fa[x][t][1][1] + dpx[1]); dpx[0] = tx[0]; dpx[1] = tx[1]; x = father[x][t]; } } if(x == y) return dpx[val2] + ff[x][val2];
这里将 x 和 y 移动到同一层
执行条件是 x 和 y 之间的距离大于 \(2^t\)
这保证了 x 不会跳过头
然后就是嫁接的部分了
这里的 tx 是 x 的 \(2^t\) 辈祖先
最后要判断 x 是否和 y 重合
因为如果重合了
y 是不能随意取的
需要满足 val2 的要求
for(int t = 20;t >= 0;t--){ if(father[x][t] != father[y][t]){ tx[0] = min(fa[x][t][0][0] + dpx[0], fa[x][t][1][0] + dpx[1]); tx[1] = min(fa[x][t][0][1] + dpx[0], fa[x][t][1][1] + dpx[1]); dpx[0] = tx[0]; dpx[1] = tx[1]; x = father[x][t]; ty[0] = min(fa[y][t][0][0] + dpy[0], fa[y][t][1][0] + dpy[1]); ty[1] = min(fa[y][t][0][1] + dpy[0], fa[y][t][1][1] + dpy[1]); dpy[0] = ty[0]; dpy[1] = ty[1]; y = father[y][t]; } }
执行条件是他们的 \(2^t\) 辈祖先不是同一个
这让循环结束后 x 和 y 在他们的 LCA 下方
这里的嫁接和上文同理 不再赘叙
int t = father[x][0]; ll lca_0 = f[t][0] - f[x][1] - f[y][1] + dpx[1] + dpy[1] + ff[t][0]; ll lca_1 = f[t][1] - min(f[x][0],f[x][1]) - min(f[y][0],f[y][1]) + min(dpx[0],dpx[1]) + min(dpy[0],dpy[1]) + ff[t][1]; return min(lca_0,lca_1);}
这里是处理返回值 和上文相同
代码
44分
//P5024 44p 注释版#include<bits/stdc++.h>#define ll long long#define maxn 100005using namespace std;int n,m,val[maxn],vis[maxn];char type[100];ll f[maxn][2];/* n 城市数量(即节点数) m 要求数量 val[i] 城市i所部署军队的耗资(即节点i的权值) vis[i] 要求的存储变量 vis[i] = 0(代表城市i不得驻军 即节点i不可取) 1(代表城市i必须驻军 即节点i必取) type[] 用来存储规模参数 f[i][j] i代表节点 j = 0(代表不取当前节点的最小子树权值和) 1(代表取当前节点的最小子树权值和)*/int cnt,head[maxn];struct tree{ int u,v; tree(int a = 0,int b = 0){ v = a; u = head[b]; }}e[maxn<<1];//邻接表存图struct Rest{ int node1,node2; int val1,val2;}rest[maxn];/* 用结构体来存储要求 node1/2存要求的节点 val1/2存必取或必不取*/void Read(){//读入 int a,b; cin >> n >> m >> type; for(int i = 1;i <= n;i++) cin >> val[i]; //存节点权值 for(int i = 1;i < n;i++){//存图 cin >> a >> b; e[++cnt] = tree(a,b); head[b] = cnt; e[++cnt] = tree(b,a); head[a] = cnt; } int x,y; for(ll i = 1;i <= m;i++){//读入要求 cin >> a >> x >> b >> y; rest[i].node1 = a; rest[i].val1 = x; rest[i].node2 = b; rest[i].val2 = y; }}void trans(int id){//在dfs前调用 预处理要求 memset(vis,2,sizeof(vis)); vis[rest[id].node1] = rest[id].val1; vis[rest[id].node2] = rest[id].val2;}ll dfs(int u,int fa){//深搜 树形dp if((vis[u]==0)&&(vis[fa]==0)) return -1; //排除不可能的情况 即父节点和子节点都取不得 不符合题意 f[u][0] = 0;//父节点不选的时候 f[u][1] = val[u];//父节点选的时候 for(int i = head[u];i;i = e[i].u){//搜每一个父向子的边 int ev = e[i].v;//ev 即子节点 if(ev == fa) continue;//防止向上爬 if(dfs(ev,u) < 0) return -1;//继续往下搜 如果不满足题意则直接返回-1 f[u][0] += f[ev][1];/* 当父节点不选的时候 子节点都必须选择 所以直接累加子节点选择时的权值 */ if(vis[ev] == 0){ //子节点不能选 则父节点必须选 f[u][1] += f[ev][0]; vis[u] = 1;//修改父节点为必选 } else if (vis[ev] == 1) { //子节点必选 则只累加子节点必选的最小子树值 f[u][1] += f[ev][1]; } else { //没有限制 则择优选择小的上报 f[u][1] = min(f[u][1] + f[ev][1],f[u][1] + f[ev][0]); }/* 当父节点选的时候 子节点可以选或不选 */ } if(vis[u] == 1) return f[u][1]; if(vis[u] == 0) return f[u][0]; return min(f[u][1],f[u][0]);/* 通过条件决定返回值 用于输出结果 */}int main(){ Read();//读入 for(int i = 1;i <= m;i++){//循环每个条件 trans(i);//读入条件 预处理 ll ans = dfs(1,0);//深搜求答案 cout << ans <<endl;//输出 } return 0;}
68分
#include<bits/stdc++.h>#define ll long long#define maxn 100005#define INF 1e12using namespace std;int n,m;int head[maxn],cnt;int val[maxn],deep[maxn],father[maxn];char type[100];ll f[maxn][2],ff[maxn][2],dp[maxn][2];struct Edge{ int u,v; Edge(int a = 0,int b = 0){ u = head[a]; v = b; }}e[maxn<<1];struct Rest{ int node1,node2; int val1,val2;}rest[maxn];void Read(){ int a,b; cin >> n >> m >> type; for(int i = 1;i <= n;i++){ cin >> val[i]; } for(int i = 1;i <= (n-1);i++){ cin >> a >> b; e[++cnt] = Edge(a,b); head[a] = cnt; e[++cnt] = Edge(b,a); head[b] = cnt; } for(int i = 1;i <= m;i++){ cin >> rest[i].node1 >> rest[i].val1; cin >> rest[i].node2 >> rest[i].val2; }}void dfs1(int u,int fa){ f[u][0] = 0; f[u][1] = val[u]; father[u] = fa; deep[u] = deep[fa] + 1; for(int i = head[u];i;i = e[i].u){ int ev = e[i].v; if(ev == fa) continue; dfs1(ev,u); f[u][0] += f[ev][1]; f[u][1] += min(f[ev][0],f[ev][1]); }}void dfs2(int u,int fa){ for(int i = head[u];i;i = e[i].u){ int ev = e[i].v; if(ev == fa) continue; ff[ev][0] = ff[u][1] + f[u][1] - min(f[ev][0],f[ev][1]); ff[ev][1] = min(ff[u][0] + f[u][0] - f[ev][1],ff[ev][0]); dfs2(ev,u); }}void trans(int id){ int a = rest[id].node1; int b = rest[id].node2; int x = rest[id].val1; int y = rest[id].val2; memset(dp,sizeof(dp),0); if(x == 0){ dp[a][0] = f[a][0]; dp[a][1] = INF; } else { dp[a][1] = f[a][1]; dp[a][0] = INF; } if(y == 0){ dp[b][0] = f[b][0]; dp[b][1] = INF; } else { dp[b][1] = f[b][1]; dp[b][0] = INF; }}ll LCAans(int x,int y){ int t; if(deep[x] < deep[y]) swap(x,y); while (deep[x] > deep[y] && father[x] != y){ t = father[x]; dp[t][1] = f[t][1] - min(f[x][0],f[x][1]) + min(dp[x][0],dp[x][1]); dp[t][0] = f[t][0] - f[x][1] + dp[x][1]; x = t; } if(father[x] == y){ dp[y][1] = dp[y][1] - min(f[x][0],f[x][1]) + min(dp[x][0],dp[x][1]); dp[y][0] = dp[y][0] - f[x][1] + dp[x][1]; return min(dp[y][1] + ff[y][1],dp[y][0] + ff[y][0]); } while(father[x] != father[y]){ t = father[x]; dp[t][1] = f[t][1] - min(f[x][0],f[x][1]) + min(dp[x][0],dp[x][1]); dp[t][0] = f[t][0] - f[x][1] + dp[x][1]; x = t; t = father[y]; dp[t][1] = f[t][1] - min(f[y][0],f[y][1]) + min(dp[y][0],dp[y][1]); dp[t][0] = f[t][0] - f[y][1] + dp[y][1]; y = t; } t = father[x]; dp[t][1] = f[t][1] - min(f[x][0],f[x][1]) + min(dp[x][0],dp[x][1]) - min(f[y][0],f[y][1]) + min(dp[y][0],dp[y][1]); dp[t][0] = f[t][0] - f[x][1] + dp[x][1] - f[y][1] + dp[y][1]; return min(dp[t][0] + ff[t][0],dp[t][1] + ff[t][1]);}int main(){ Read(); dfs1(1,0); dfs2(1,0); for(int i = 1;i <= m;i++){ trans(i); ll res = LCAans(rest[i].node1,rest[i].node2); if(res < INF) cout << res << endl; else cout << "-1" << endl; } return 0;}
100分
#include<bits/stdc++.h>#define ll long long#define maxn 100005#define INF 1e12using namespace std;int n,m,val[maxn];int head[maxn],cnt;int deep[maxn],father[maxn][25];char type[100];ll dpx[2],dpy[2];ll f[maxn][2],ff[maxn][2];ll fa[maxn][25][2][2];struct Edge{ int u,v; Edge(int a = 0,int b = 0){ u = head[a]; v = b; }}e[maxn<<1];struct Rest{ int node1,node2; int val1,val2;}rest[maxn];void Read(){ int a,b; cin >> n >> m >> type; for(int i = 1;i <= n;i++) cin >> val[i]; for(int i = 1;i < n;i++){ cin >> a >> b; e[++cnt] = Edge(a,b); head[a] = cnt; e[++cnt] = Edge(b,a); head[b] = cnt; } for(int i = 1;i <= m;i++){ cin >> rest[i].node1 >> rest[i].val1; cin >> rest[i].node2 >> rest[i].val2; }}void dfs1(int u,int fa){ f[u][0] = 0; f[u][1] = val[u]; father[u][0] = fa; deep[u] = deep[fa] + 1; for(int i = head[u];i;i = e[i].u){ int ev = e[i].v; if(ev == fa) continue; dfs1(ev,u); f[u][0] += f[ev][1]; f[u][1] += min(f[ev][1],f[ev][0]); }}void dfs2(int u,int fa){ for(int i = head[u];i;i = e[i].u){ int ev = e[i].v; if(ev == fa) continue; ff[ev][0] = ff[u][1] + f[u][1] - min(f[ev][0],f[ev][1]); ff[ev][1] = min(ff[u][0] + f[u][0] - f[ev][1],ff[ev][0]); dfs2(ev,u); }}void LCA(){ for(int i = 1;i <= n;i++){ int t = father[i][0]; fa[i][0][0][0] = INF; fa[i][0][0][1] = f[t][1] - min(f[i][0],f[i][1]); fa[i][0][1][0] = f[t][0] - f[i][1]; fa[i][0][1][1] = fa[i][0][0][1]; } for(int t = 1;t <= 20;t++){ for(int i = 1;i <= n;i++){ int X = father[i][t-1]; father[i][t] = father[X][t-1]; fa[i][t][0][0] = min(fa[i][t-1][0][0] + fa[X][t-1][0][0], fa[i][t-1][0][1] + fa[X][t-1][1][0]); fa[i][t][0][1] = min(fa[i][t-1][0][0] + fa[X][t-1][0][1], fa[i][t-1][0][1] + fa[X][t-1][1][1]); fa[i][t][1][0] = min(fa[i][t-1][1][0] + fa[X][t-1][0][0], fa[i][t-1][1][1] + fa[X][t-1][1][0]); fa[i][t][1][1] = min(fa[i][t-1][1][0] + fa[X][t-1][0][1], fa[i][t-1][1][1] + fa[X][t-1][1][1]); } }}ll LCAans(int x,int y,int val1,int val2){ ll tx[2] = {0,0}; ll ty[2] = {0,0}; dpx[0] = dpx[1] = INF; dpy[0] = dpy[1] = INF; if(deep[x] < deep[y]){ swap(x,y); swap(val1,val2); } dpx[val1] = f[x][val1]; dpy[val2] = f[y][val2]; for(int t = 20;t >= 0;t--){ if((deep[x] - deep[y]) >= (1<<t)){ tx[0] = min(fa[x][t][0][0] + dpx[0], fa[x][t][1][0] + dpx[1]); tx[1] = min(fa[x][t][0][1] + dpx[0], fa[x][t][1][1] + dpx[1]); dpx[0] = tx[0]; dpx[1] = tx[1]; x = father[x][t]; } } if(x == y) return dpx[val2] + ff[x][val2]; for(int t = 20;t >= 0;t--){ if(father[x][t] != father[y][t]){ tx[0] = min(fa[x][t][0][0] + dpx[0], fa[x][t][1][0] + dpx[1]); tx[1] = min(fa[x][t][0][1] + dpx[0], fa[x][t][1][1] + dpx[1]); dpx[0] = tx[0]; dpx[1] = tx[1]; x = father[x][t]; ty[0] = min(fa[y][t][0][0] + dpy[0], fa[y][t][1][0] + dpy[1]); ty[1] = min(fa[y][t][0][1] + dpy[0], fa[y][t][1][1] + dpy[1]); dpy[0] = ty[0]; dpy[1] = ty[1]; y = father[y][t]; } } int t = father[x][0]; ll lca_0 = f[t][0] - f[x][1] - f[y][1] + dpx[1] + dpy[1] + ff[t][0]; ll lca_1 = f[t][1] - min(f[x][0],f[x][1]) - min(f[y][0],f[y][1]) + min(dpx[0],dpx[1]) + min(dpy[0],dpy[1]) + ff[t][1]; return min(lca_0,lca_1);}int main(){ Read(); dfs1(1,0); dfs2(1,0); LCA(); for(int i = 1;i <= m;i++){ ll res = LCAans(rest[i].node1,rest[i].node2,rest[i].val1,rest[i].val2); if(res < INF) cout << res << endl; else cout << "-1" <<endl; } return 0;}