堆是什么
堆是一种特殊的完全二叉树
如果你是初学者,你的表情一定是这样的??
别想复杂
首先,你一定见过这种图

咱们暂时不管数字
这就是一个堆
堆又分为最大堆和最小堆
最大堆
看这张图
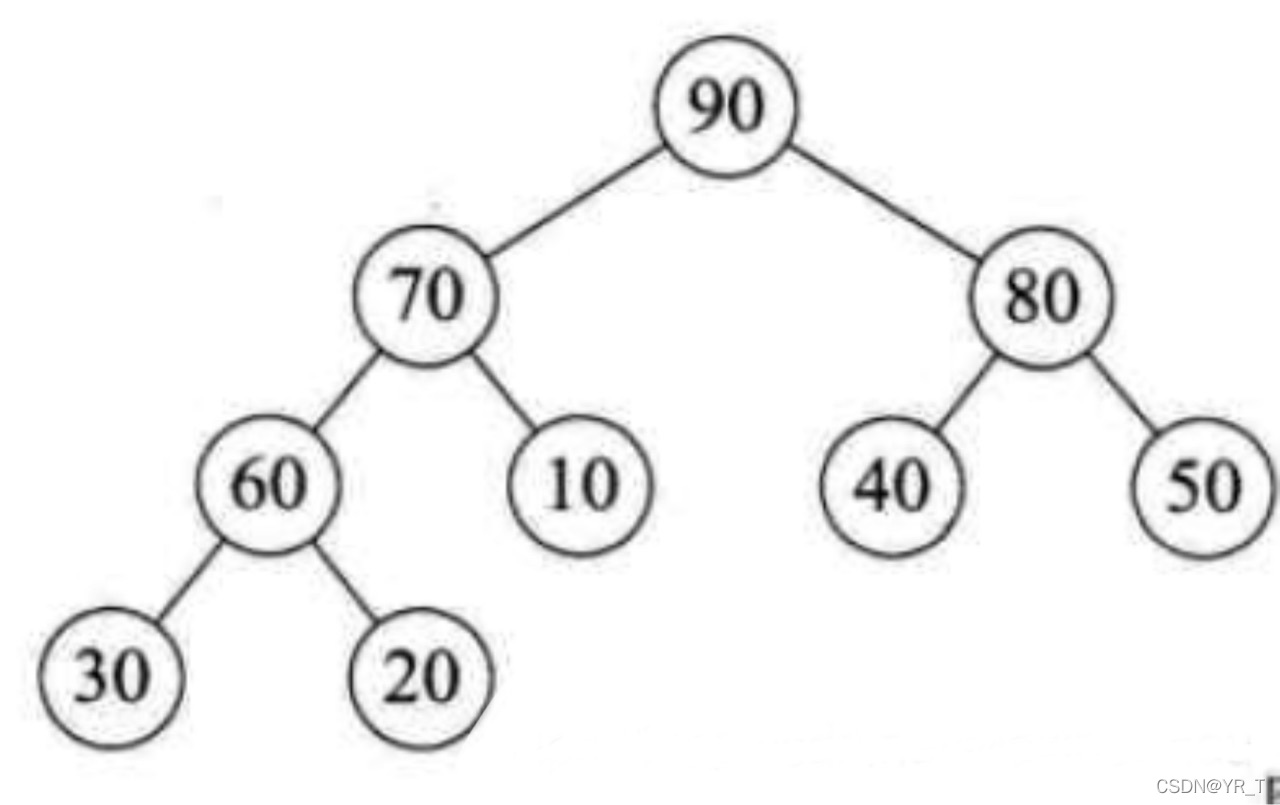
上面的节点的数都比下面的节点的数大,最上面的数是最大的,这就叫最大堆??
最小堆
还是一样的数,看这张图

这是一个最小堆,同最大堆,最上面的节点的数最小,上面的节点的数比下面的节点的数大
怎么样,是不是很简单?
堆排序
堆排序的基本思想是利用堆,使在排序中比较的次数明显减少使速度更快
堆排序的时间复杂度为O(n*log(n)), 非稳定排序,原地排序(空间复杂度O(1))。
堆排序的关键在于建堆和调整堆,下面简单介绍一下建堆的过程:
可以用STL下的
make_heap()
具体步骤:
第1趟将索引0至n-1处的全部数据建大顶(或小顶)堆,就可以选出这组数据的最大值(或最小值)。将该堆的根节点与这组数据的最后一个节点交换,就使的这组数据中最大(最小)值排在了最后。
第2趟将索引0至n-2处的全部数据建大顶(或小顶)堆,就可以选出这组数据的最大值(或最小值)。将该堆的根节点与这组数据的倒数第二个节点交换,就使的这组数据中最大(最小)值排在了倒数第2位。
…
第k趟将索引0至n-k处的全部数据建最大(或最小)堆,就可以选出这组数据的最大值(或最小值)。将该堆的根节点与这组数据的倒数第k个节点交换,就使的这组数据中最大(最小)值排在了倒数第k位。
其实整个堆排序过程中, 我们只需重复做两件事:
建堆(初始化+调整堆, 时间复杂度为O(n));
拿堆的根节点和最后一个节点交换(siftdown, 时间复杂度为O(n*log n) ).
因而堆排序整体的时间复杂度为O(n*log n)
没看懂可以看看这个图

最终代码
- #include <iostream>
- #include <stdlib.h>
- using namespace std;
-
- /*******************************************/
- /* 堆排序
- /******************************************/
-
- void swap(int &a, int &b) //位置互换函数
- {
- int temp = a;
- a = b;
- b = temp;
- }
-
-
- void Heap(int array[], int length, int index) //堆排序算法(大顶堆)
- {
- int left = 2 * index + 1; //左节点数组下标
- int right = 2 * index + 2; //右节点数组下标
- int max = index; //index是父节点
-
- if (left < length && array[left] > array[max]) //左节点与父节点比较
- {
- max = left;
- }
-
- if (right < length && array[right] > array[max]) //右节点与父节点比较
- {
- max = right;
- }
-
- if (array[index] != array[max])
- {
- swap(array[index], array[max]);
- Heap(array, length, max); //递归调用
- }
- }
-
-
- void HeapSort(int array[], int size) //堆排序函数
- {
- for (int i = size / 2 - 1; i >= 0; i--) // 创建一个堆
- {
- Heap(array, size, i);
- }
-
- for (int i = size - 1; i >= 1; i--)
- {
- swap(array[0], array[i]); //将array[0]的最大值放到array[i]的位置上,最大值往后靠
- Heap(array, i, 0); //调用堆排序算法进行比较
- }
- }
-
-
- int main(void) //主程序
- {
- const int n = 6; //数组元素的数量
- int array[n];
- cout << "请输入6个整数:" << endl;
- for (int i = 0; i < n; i++)
- {
- cin >> array[i];
- }
-
- cout << endl; //换行
-
- HeapSort(array, n); // 调用HeapSort函数 进行比较
-
- cout << "由小到大的顺序排列后:" << endl;
- for (int i = 0; i < n; i++)
- {
- cout << "Array" << "[" << i << "]" << " = " << array[i] << endl;
- }
-
- cout << endl << endl; //换行
-
- system("pause"); //调试时,黑窗口不会闪退,一直保持
- return 0;
- }
关于堆
C++中堆的应用:make_heap, pop_heap, push_heap, sort_heap
函数说明: make_heap将[start, end)范围进行堆排序,默认使用less, 即最大元素放在第一个。
pop_heap将front(即第一个最大元素)移动到end的前部,同时将剩下的元素重新构造成(堆排序)一个新的heap。
push_heap对刚插入的(尾部)元素做堆排序。
sort_heap将一个堆做排序,最终成为一个有序的系列,可以看到sort_heap时,必须先是一个堆(两个特性:1、最大元素在第一个 2、添加或者删除元素以对数时间),因此必须先做一次make_heap.
到此这篇关于c++深入浅出讲解堆排序和堆的文章就介绍到这了,更多相关c++ 堆排序内容请搜索w3xue以前的文章或继续浏览下面的相关文章希望大家以后多多支持w3xue!