C++数据结构之二叉搜索树的实现详解

来源：jb51　　时间：2022/8/22 16:17:57　　对本文有异议

前言

今天我们来学一个新的数据结构：二叉搜索树。

介绍

二叉搜索树也称作二叉排序树，它具有以下性质：

非空左子树的所有键值小于其根节点的键值
非空右子树的所有键值大于其根节点的键值
左，右子树都是二叉搜索树

那么我先画一个二叉搜索树给大家看看，是不是真的满足上面的性质。

我们就以根节点6为例子来看，我们会发现比6小的都在6的左边，而比6大的都在6的右边。对于6的左右子树来说，所有的节点都遵循这个规则。

同时我们还可以发现如果对搜索二叉树进行一个中序遍历，我们得到的序列是个有序序列，这就是为什么二叉搜索树也可以称作二叉排序树。

实现

节点的实现

template <typename K>
struct BTreeNode
{
	BTreeNode<K>* _left;
	BTreeNode<K>* _right;
	K _key;
 
	BTreeNode(const K& key)
		:_key(key), _left(nullptr), _right(nullptr)
	{}
};

二叉搜索树的查找

二叉搜索树的查找思路很简单：要找的值比当前节点小就去左子树找，比当前节点大就往右子树找，找到空节点就说明没找到返回false即可。

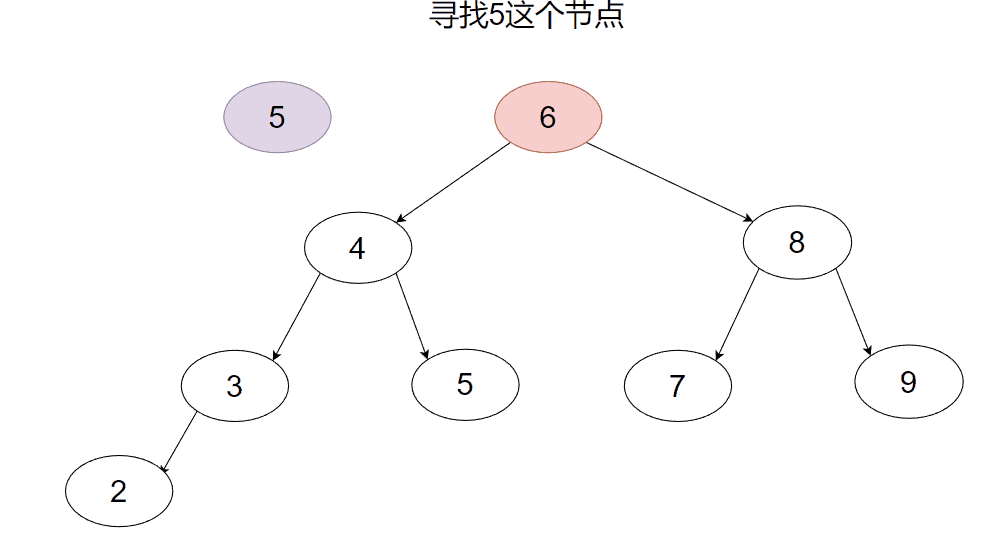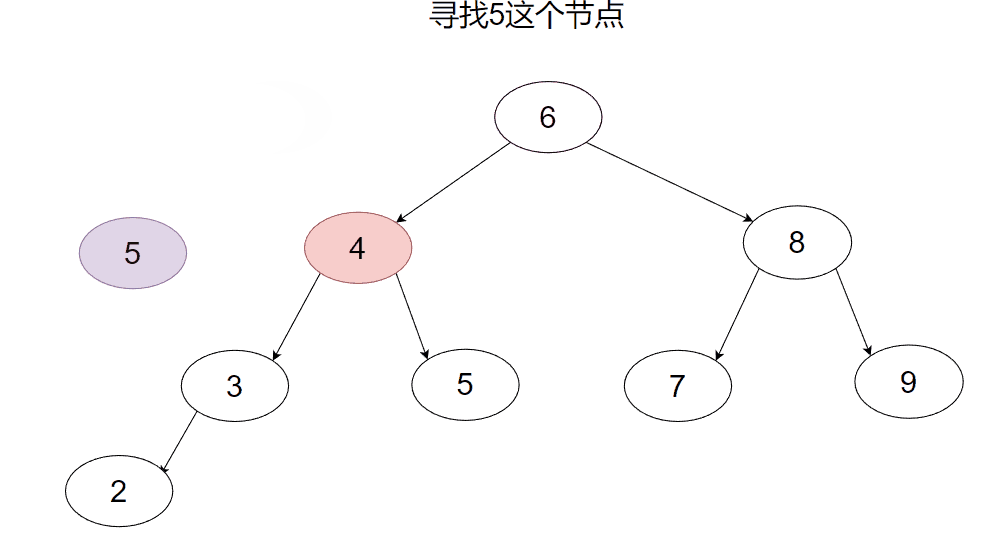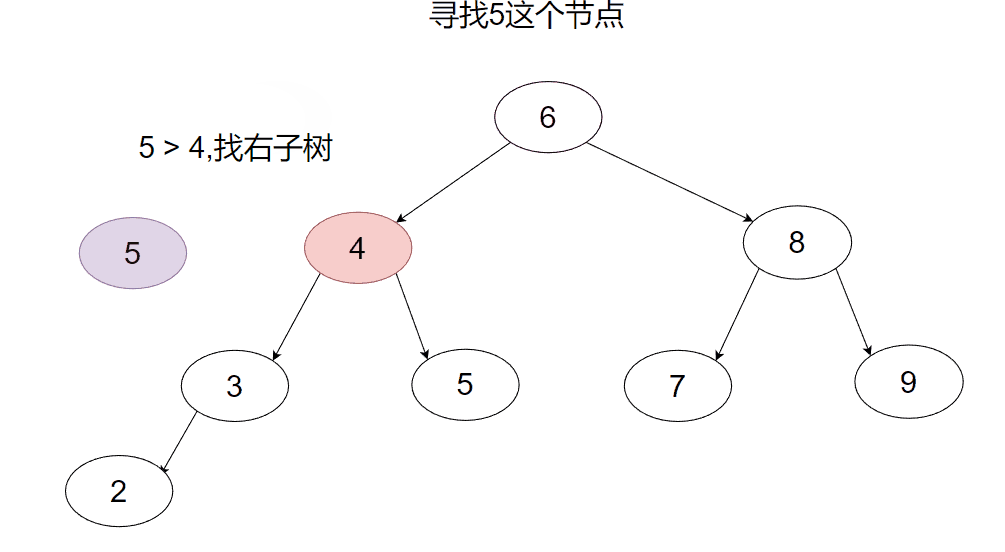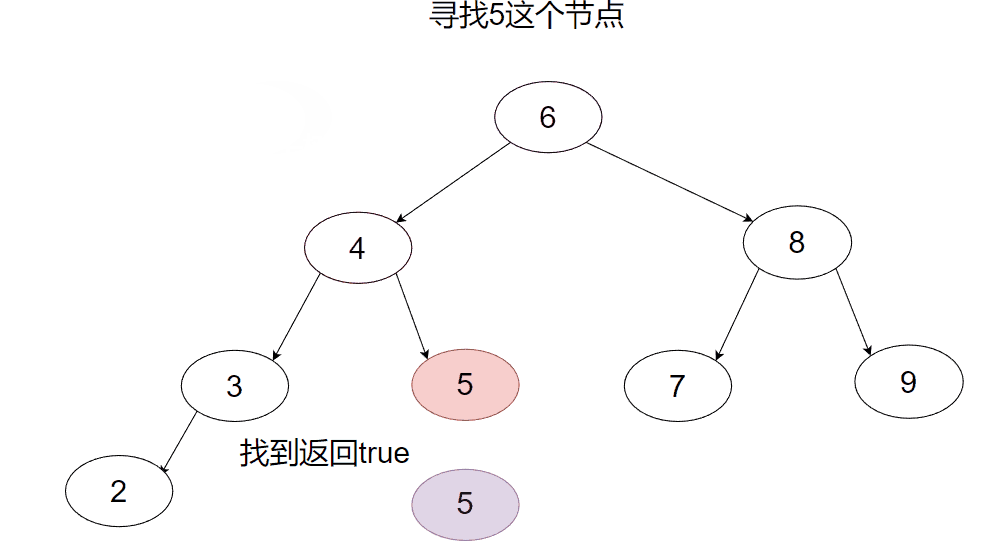
首先我们先看看递归的版本。

bool findR(const T &val, Node *root) //T为节点的K, Node为节点
{
    if (root == nullptr)
    {
        return false;
    }
 
    if (root->_key < val)
    {
        return findR(root->_right, val);
    }
    else if (root->_key > val)
    {
        return findR(root->_left, val);
    }
    else
    {
        return true;
    }
}

接着看看非递归的版本

bool find(const T &val)
{
    Node *cur = _root; //_root为二叉搜索树的根节点
    while (cur)
    {
        if (val < cur->_key)
        {
            cur = cur->_left;
        }
        else if (val > cur->_key)
        {
            cur = cur->_right;
        }
        else
        {
            return true;
        }
    }
    return false;
}

二叉搜索树的插入

二叉搜索树的插入和查找差别不大，首先寻找插入位置，比当前节点小就往左子树找，比当前节点大就往右子树找，直到找到空指针时，就可以进行一个插入。

那么要插入的值和当前节点相同该怎么办呢？我们此时实现的二叉搜索树是一个无重复元素的二叉搜索树，所以对于相同的值我采取的方式是返回一个false，大家如果想实现一个有重复元素的二叉搜索树，可以选择将重复的值放在右子树或左子树都可。

二叉搜索树的插入和查找一样，有递归和非递归两个版本，首先我们先来看看非递归的版本。

bool insert(const T &val)
{
    //空树直接改变根节点
    if (_root == nullptr)
    {
        _root = new Node(val);
        return true;
    }
    
     //非空树先寻找插入位置
    Node *pre = nullptr;
    Node *cur = _root;
    while (cur)
    {
        if (val > cur->_key)
        {
            pre = cur;
            cur = cur->_right;
        }
        else if (val < cur->_key)
        {
            pre = cur;
            cur = cur->_left;
        }
        else
        {
            return false;
        }
    }
    //判断新节点该插入到哪里
    cur = new Node(val);
    if (val < pre->_key)
    {
        pre->_left = cur;
    }
    else
    {
        pre->_right = cur;
    }
    return true;
}

接下来用一个动画来表示一下这个插入过程。

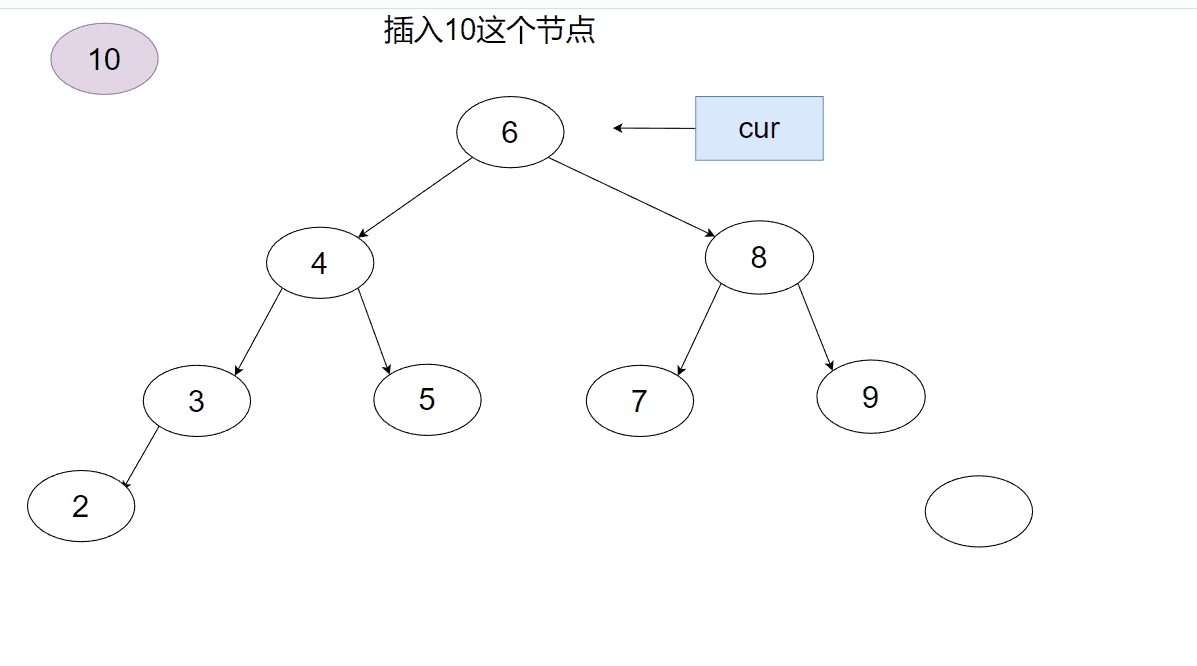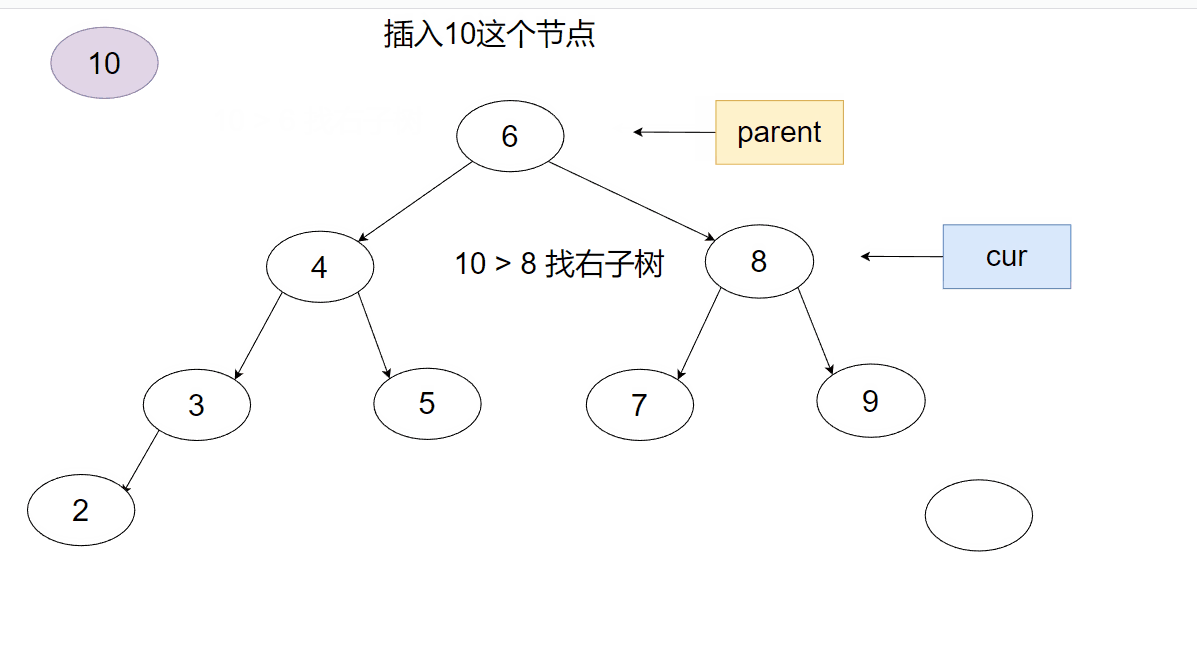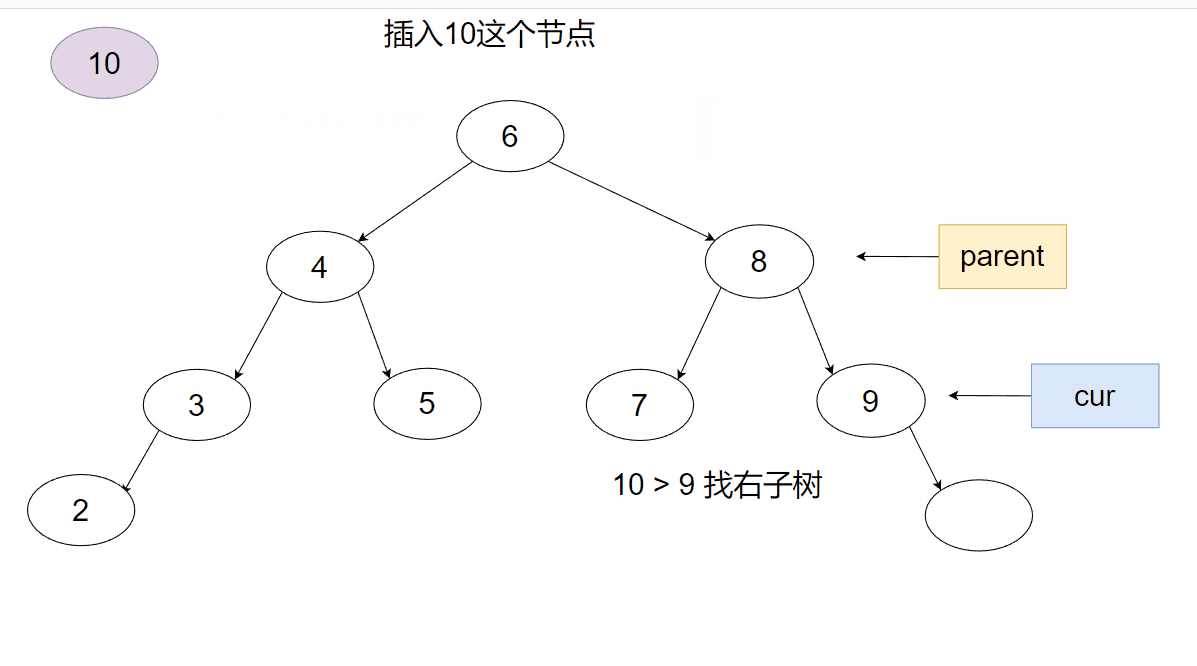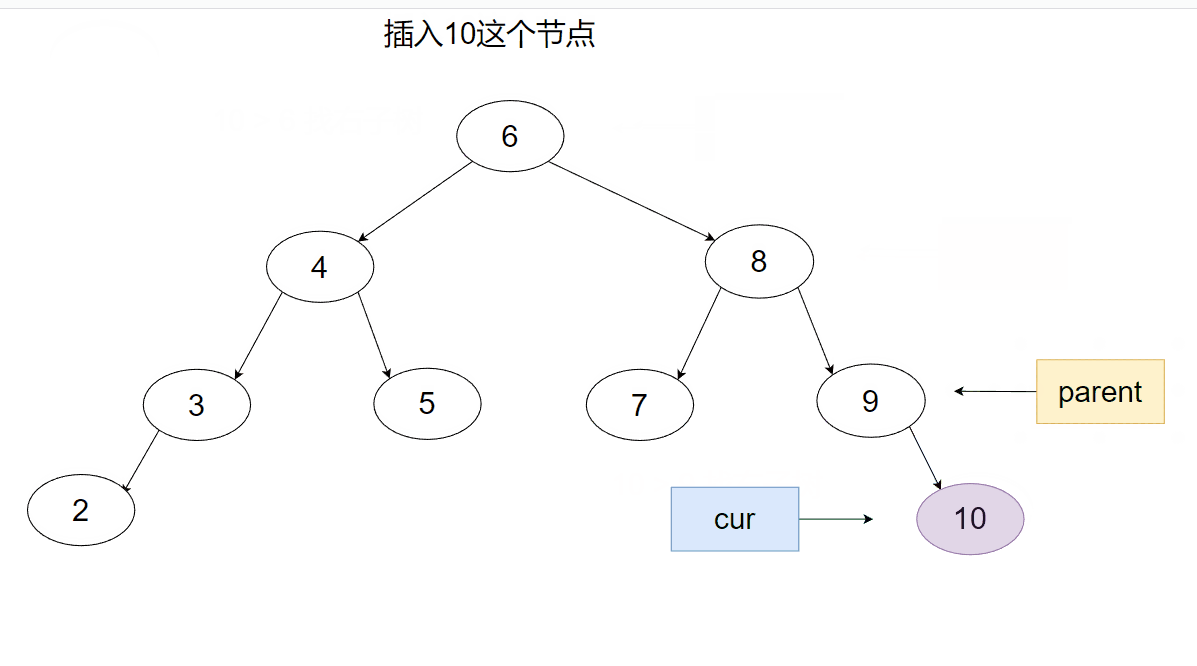
接下来我们来看看递归版本是如何实现的

bool insertR(const T &val, Node *&root)
{
    if (root == nullptr)
    {
        Node *newNode = new Node(val);
        root = newNode;
    }
 
    if (root->_key < val)
    {
        return insertR(val, root->_right);
    }
    else if (root->_key > val)
    {
        return insertR(val, root->_left);
    }
    else
    {
        return false;
    }
}

此时我们可以发现，递归版本没有非递归版本中的parent指针了，参数列表中只有一个root指针，这是为什么呢？

我们可以看见我们的root指针不仅是一个指针，同时它还是一个引用。这就意味着我们对root的修改也可以影响上一层传递过来的指针的值。所以此时我们不需要parent指针，就可以对上一个节点的指针进行一个修改。

二叉搜索树的删除

理论部分：

二叉搜索树的删除相比前面两个要麻烦那么一丢丢，首先当然是找要删除的节点，找到后通常有以下三种情况：

此节点无左右子树
此节点有右子树或右子树
此节点有左右子树

我们要做的就是对这三种情况分别进行一个处理。

1.首先是此节点无左右子树，这种情况我们直接将此节点删除即可

2.然后是此节点只有一颗子树，这个也比较简单，如果此节点是父节点的左节点，那么我们只需要将父节点的左指针改成指向此节点的子树即可。

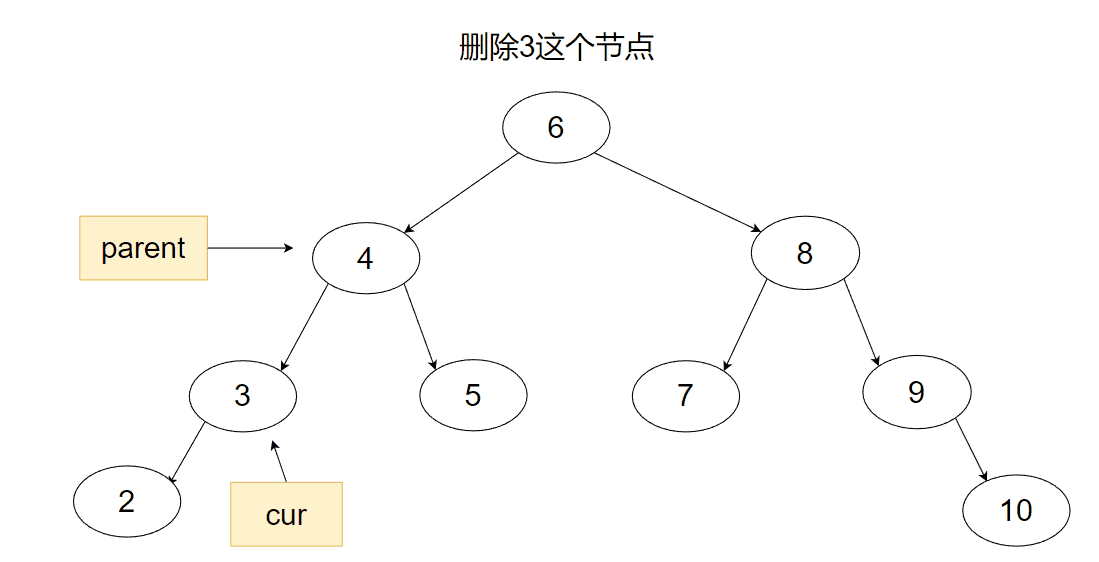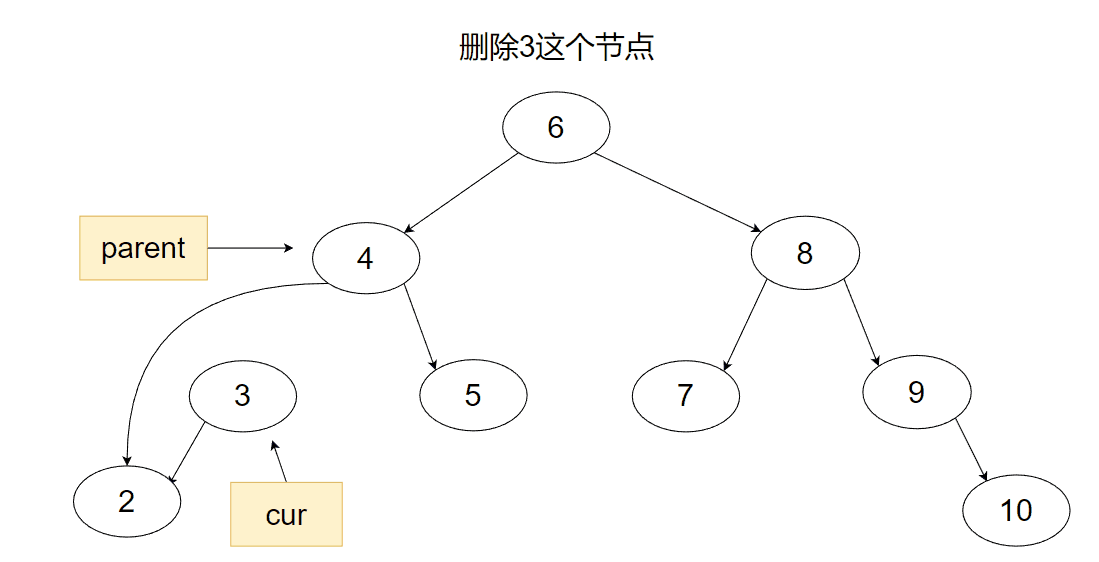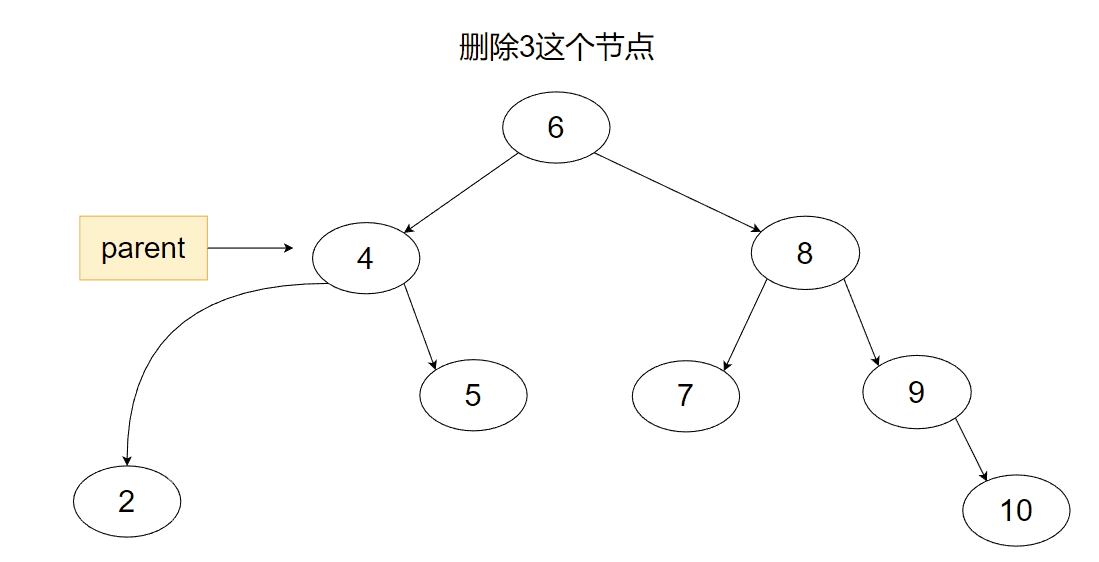
3.最后一种就是既有左子树又有右子树的情况了，此时为了不破坏结构，我们需要用到替换删除法。首先我们先找到要删除的节点，然后找节点的左子树的最右节点或右子树的最左节点，将两个节点进行一下互换，再将原节点删除。

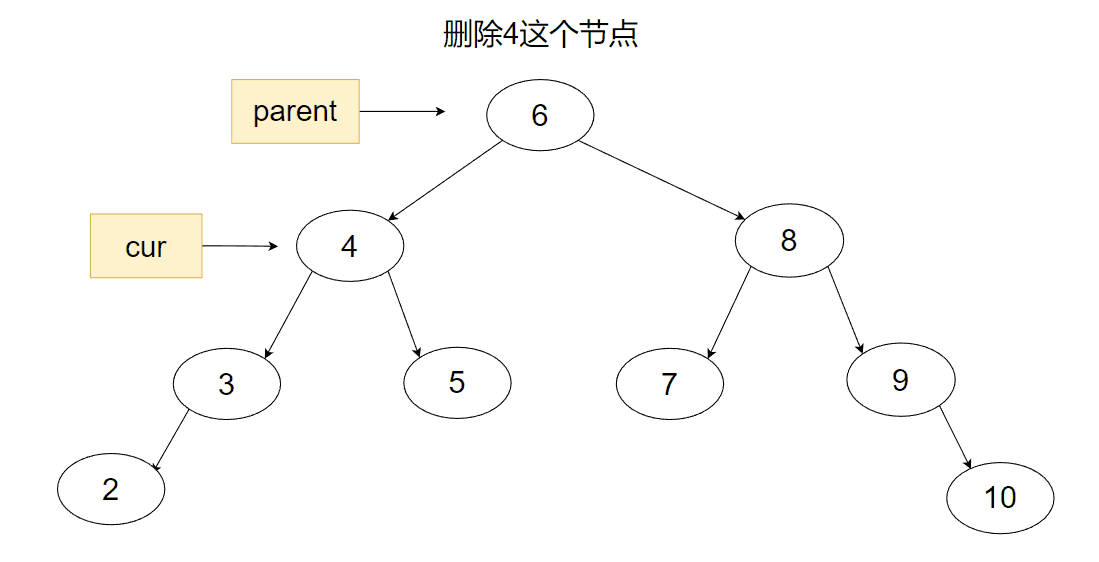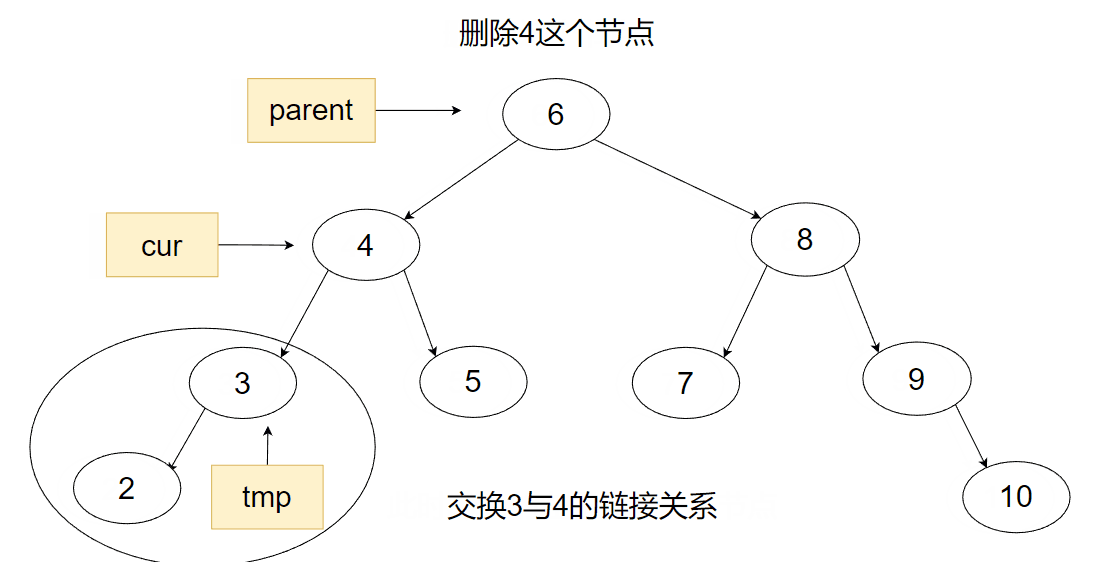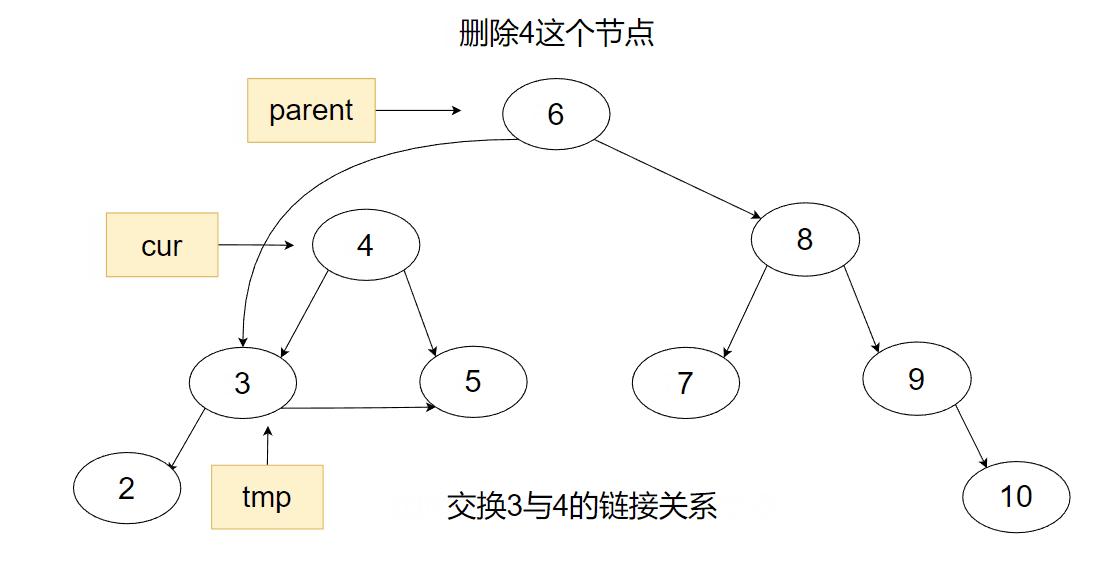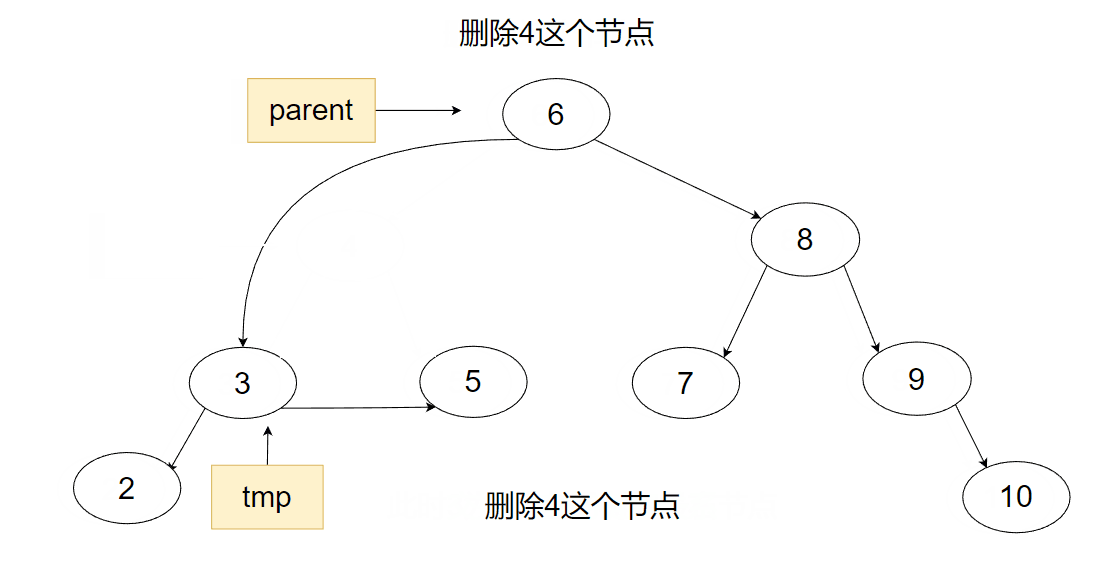
代码部分：

首先是非递归版本

bool erase(const T &val)
{
    Node *cur = _root;
    Node *pre = nullptr;
    //寻找删除位置
    while (cur)
    {
        if (cur->_key < val)
        {
            pre = cur;
            cur = cur->_right;
        }
        else if (cur->_key > val)
        {
            pre = cur;
            cur = cur->_left;
        }
        else //找到了进行删除
        {
            if (cur->_left == nullptr) //左子树为空
            {
                if (cur == _root)
                {
                    _root = cur->_right;
                }
                else
                {
                    if (cur == pre->_left)
                    {
                        pre->_left = cur->_right;
                    }
                    else
                    {
                        pre->_right = cur->_right;
                    }
                }
                delete cur;
            }
            else if (cur->_right == nullptr) //右子树为空
            {
                if (cur == _root)
                {
                    _root = cur->_left;
                }
                else
                {
                    if (cur == pre->_left)
                    {
                        pre->_left = cur->_left;
                    }
                    else
                    {
                        pre->_right = cur->_left;
                    }
                }
                delete cur;
            }
            else //左右子树都不为空
            {
                //找左子树的最右节点
                Node *tmp = cur->_left;
                Node *tmp_pre = cur;
                while (tmp->_right) 
                {
                    tmp_pre = tmp;
                    tmp = tmp->_right;
                }
				//节点互换
                cur->_key = tmp->_key;
 
                if (tmp == tmp_pre->_left)
                {
                    tmp_pre->_left = tmp->_left;
                }
                else
                {
                    tmp_pre->_right = tmp->_left;
                }
 
                delete tmp;
            }
            return true;
        }
    }
    return false;
}

接下来是递归版本

bool eraseR(const T &val, Node *&root)
{
    //找不到返回false
    if (root == nullptr)
    {
        return false;
    }
	//寻找插入位置
    if (root->_key < val)
    {
        return eraseR(val, root->_right);
    }
    else if (root->_key > val)
    {
        return eraseR(val, root->_left);
    }
    else
    {
        if (root->_left == nullptr)//左子树为空
        {
            root = root->_right;
        }
        else if (root->_right == nullptr)//右子树为空
        {
            root = root->_left;
        }
        else //左右子树都不为空
        {
            Node *cur = root->_left;
            while (cur->_right)
            {
                cur = cur->_right;
            }
            swap(cur->_key, root->_key);
            return eraseR(val, root->_left);
        }
        return true;
    }
}