C++利用用埃式筛法求解素数

来源：jb51　　时间：2023/1/6 8:52:24　　对本文有异议

埃式筛法

首先要了解什么式埃式筛法之前，需要知道一个定理。

就是素数的整数倍一定不是素数。

了解了这个就基本大概懂了埃式筛法。

首先初始化一个布尔数组is_prime，用于记录每个数是否为素数。
从2开始，枚举每个数i，如果is_prime[i]为true，则i是素数，添加到素数数组primes中。
然后对于每个i，我们让我扩大j倍，直到i*j小于输入的数字n，把is_prime[i * j]赋值为false。
重复步骤2和3，直到遍历到n为止。

埃式筛法求解某一个数字包含的所有素数数组

Code

#include <iostream>
#include <vector>
#include <ctime>
 
using namespace std;
 
vector <int> sieve_of_eratosthenes(int n) {
	vector <int> primes;
	vector <bool> is_prime(n + 1, true);
	is_prime[0] = is_prime[1] = false;
	for (int i = 2; i <= n; i++) {
		if (is_prime[i]) {
			primes.push_back(i);
		}
		for (int j = 2; i * j <= n; j++) {
			is_prime[i * j] = false;
		}
	}
	return primes;
}
int main() {
	clock_t start, end;
	start = clock();
	int n;
	cout << "Please Enter n: ";
	cin >> n;
 
	vector <int> primes = sieve_of_eratosthenes(n);
	cout << "Primes: ";
	for (int prime : primes) {
		cout << prime << " ";
	}
	cout << "\n素数个数为" << primes.size() << "个\n";
	end = clock();
	cout << "The run time is: " << (double)(end - start) / CLOCKS_PER_SEC << "s" << endl;
	return 0;
}

运行结果

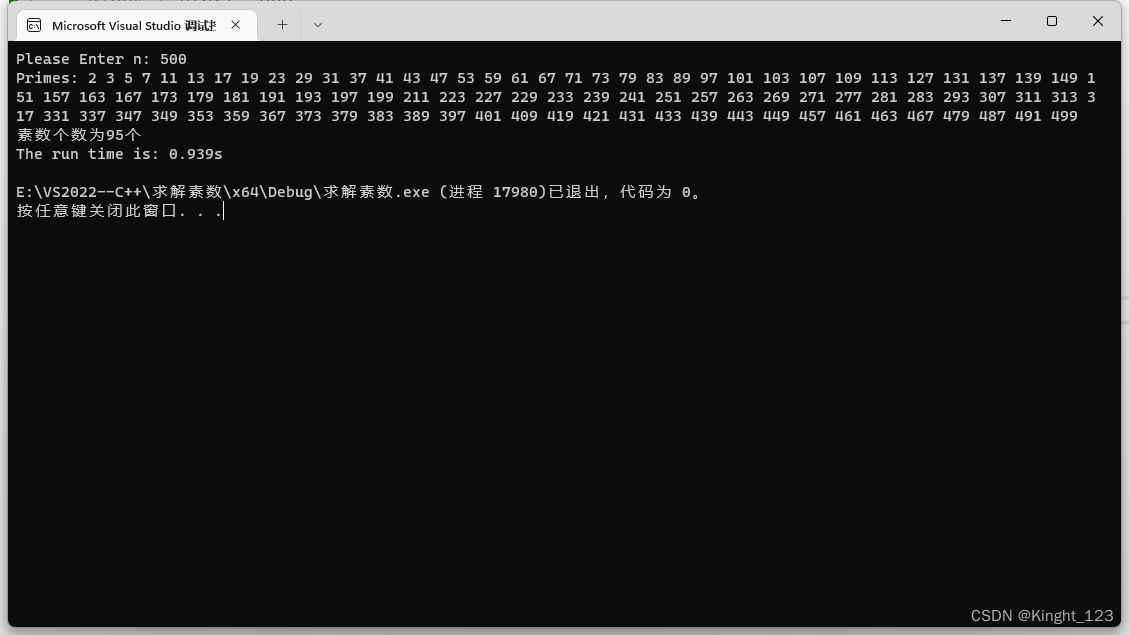
埃式筛法判断某一个数字是否为素数

Code

#include <iostream>
#include <vector>
#include <ctime>
 
using namespace std;
 
// 埃式筛法求解素数
bool sieve_of_eratosthenes(int n) {
	vector <bool> is_prime(n + 1, true);
	is_prime[0] = is_prime[1] = false;
	for (int i = 2; i <= n; i++) {
		if (is_prime[i] && i == n) {
			return true;
		}
		for (int j = 2; i * j <= n; j++) {
			is_prime[i * j] = false;
			if (i * j == n) {
				return false;
			}
		}
	}
}
int main() {
	clock_t start, end;
	start = clock();
 
	int n;
	cout << "Please Enter n: ";
	cin >> n;
	if (sieve_of_eratosthenes(n)) {
		cout << n << "是素数!!!";
	}
	else {
		cout << n << "不是素数...";
	}
	end = clock();
	cout << "The run time is: " << (double)(end - start) / CLOCKS_PER_SEC << "s" << endl;
	return 0;
}