冒泡排序
冒泡排序是一种简单的排序算法。它重复地走访过要排序的数列,一次比较两个元素,如果它们的顺序错误就把它们交换过来。走访数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。
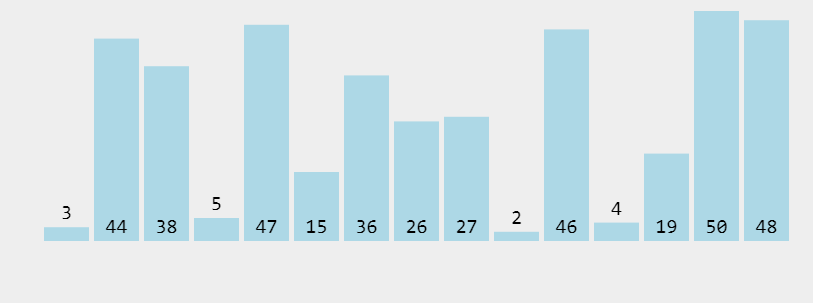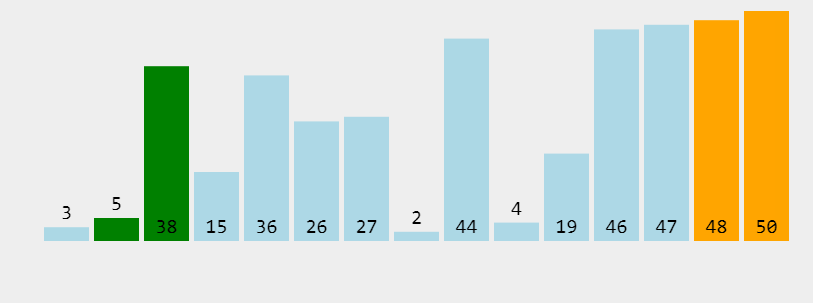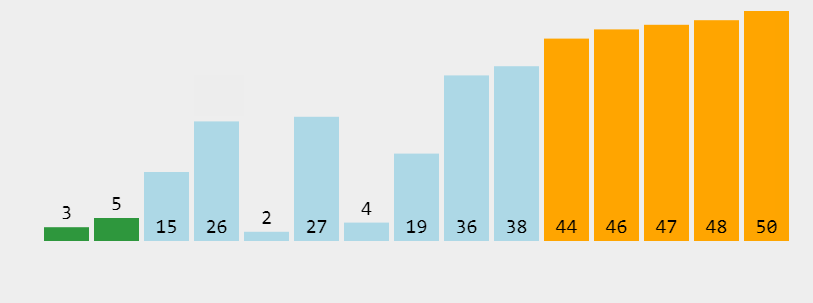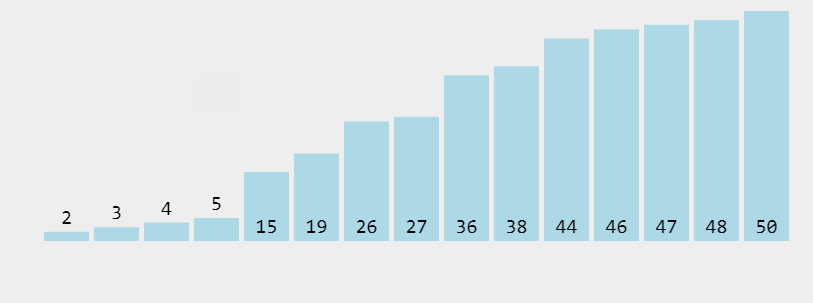
- def mao(lst):
- for i in range(len(lst)):
- # 由于每一轮结束后,总一定有一个大的数排在后面
- # 而且后面的数已经排好了
- # 即i轮之后,就有i个数字被排好
- # 所以其 len-1 -i到 len-1的位置是已经排好的了
- # 只需要比较0到len -1 -i的位置即可
-
- # flag 用于标记是否刚开始就是排好的数据
- # 只有当flag状态发生改变时(第一次循环就可以确定),继续排序,否则返回
- flag = False
- for j in range(len(lst) - i - 1):
- if lst[j] > lst[j + 1]:
- lst[j], lst[j + 1] = lst[j + 1], lst[j]
- flag = True
- # 非排好的数据,改变flag
- if not flag:
- return lst
- return lst
-
- print(mao([1, 5, 55, 4, 5, 1, 3, 4, 5, 8, 62, 7]))
选择排序
选择排序是一种简单直观的排序算法。它的工作原理:首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置,然后,再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。以此类推,直到所有元素均排序完毕。

- # 选择排序是从前开始排的
- # 选择排序是从一个列表中找出一个最小的元素,然后放在第一位上。
- # 冒泡排序类似
- # 其 0 到 i的位置是排好的,只需要排i+1到len(lst)-1即可
-
- def select_sort(lst):
- for i in range(len(lst)):
- min_index = i # 用于记录最小的元素的索引
- for j in range(i + 1, len(lst)):
- if lst[j] < lst[min_index]:
- min_index = j
-
- # 此时,已经确定,min_index为 i+1 到len(lst) - 1 这个区间最小值的索引
- lst[i], lst[min_index] = lst[min_index], lst[i]
-
- return lst
-
-
- def select_sort2(lst):
- # 第二种选择排序的方法
- # 原理与第一种一样
- # 不过不需要引用中间变量min_index
- # 只需要找到索引i后面的i+1到len(lst)的元素即可
-
- for i in range(len(lst)):
- for j in range(len(lst) - i):
-
- # lst[i + j]是一个i到len(lst)-1的一个数
- # 因为j <= len(lst) -i 即 j + i <= len(lst)
- if lst[i] > lst[i + j]:
- # 说明后面的数更小,更换位置
- lst[i], lst[i + j] = lst[i + j], lst[i]
- return lst
-
-
- print(select_sort([1, 5, 55, 4, 5, 1, 3, 4, 5, 8, 62, 7]))
- print(select_sort2([1, 5, 55, 4, 5, 1, 3, 4, 5, 8, 62, 7]))
快速排序
快速排序是通过一趟排序将待排记录分隔成独立的两部分,其中一部分记录的关键字均比另一部分的关键字小,则可分别对这两部分记录继续进行排序,以达到整个序列有序。
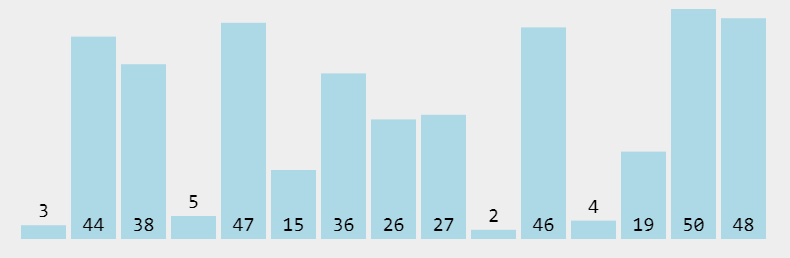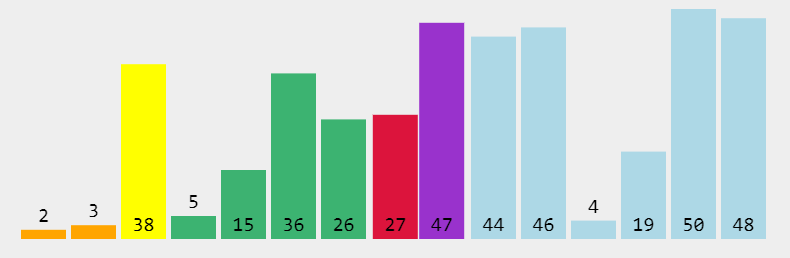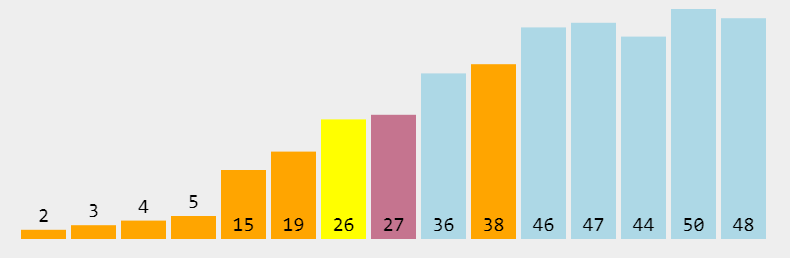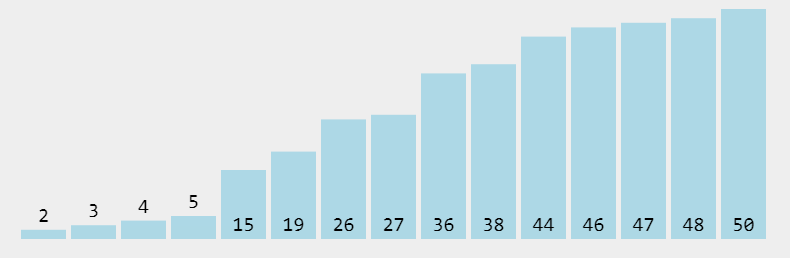
- # 原理
- # 1. 任取列表中的一个元素i
- # 2. 把列表中大于i的元素放于其右边,小于则放于其左边
- # 3. 如此重复
- # 4. 直到不能在分,即只剩1个元素了
- # 5. 然后将这些结果组合起来
-
- def quicksort(lst):
- if len(lst) < 2: # lst有可能为空
- return lst
-
- # ['pɪvət] 中心点
- pivot = lst[0]
- less_lst = [i for i in lst[1:] if i <= pivot]
- greater_lst = [i for i in lst[1:] if i > pivot]
- # 最后的结果就是
- # 左边的结果 + 中间值 + 右边的结果
- # 然后细分 左+中+右 + 中间值 + 左 + 中+ 右
- # ........... + 中间值 + ............
- return quicksort(less_lst) + [pivot] + quicksort(greater_lst)
-
-
- print(quicksort([1, 5, 55, 4, 5, 1, 3, 4, 5, 8, 62, 7]))
- print(quicksort([1, 5, 8, 62]))
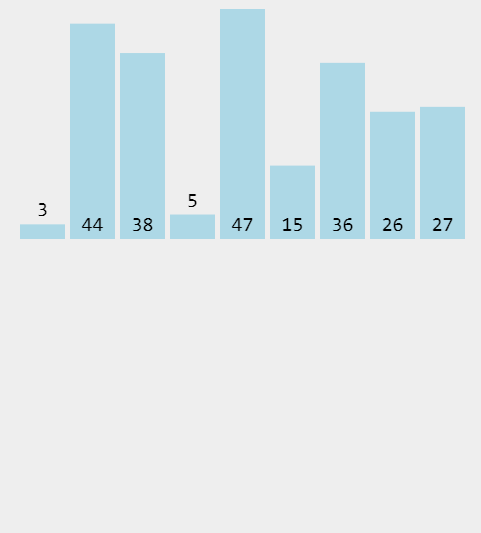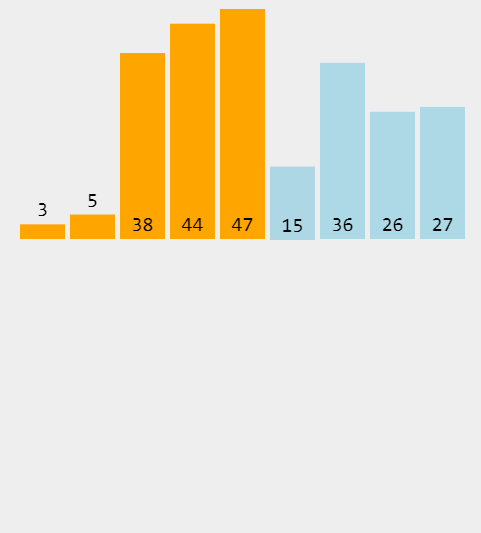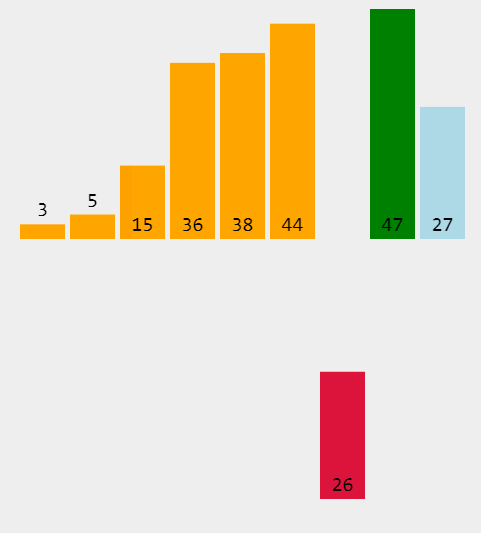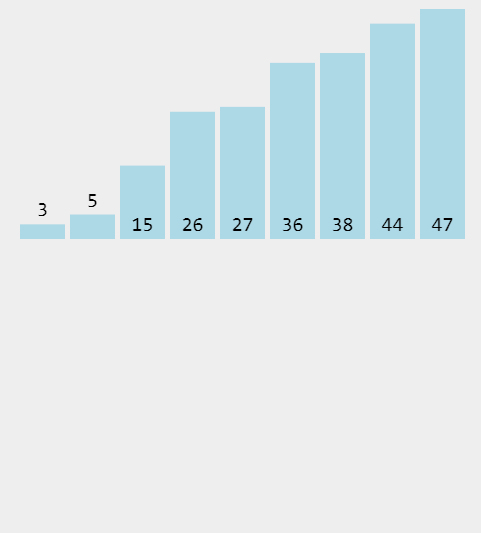
插入排序
插入排序的算法描述是一种简单直观的排序算法。它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。
- # lst的[0, i) 项是有序的,因为已经排过了
- # 那么只需要比对第i项的lst[i]和lst[0 : i]的元素大小即可
- # 假如,lst[i]大,则不用改变位置
- # 否则,lst[i]改变位置,插到j的位置,而lst[j]自然往后挪一位
- # 然后再删除lst[i+1]即可(lst[i+1]是原来的lst[i])
- #
- # 重复上面步骤即可,排序完成
-
- def insert_sort(lst: list):
- # 外层开始的位置从1开始,因为从0开始都没得排
- # 只有两个元素以上才能排序
- for i in range(1, len(lst)):
- # 内层需要从0开始,因为lst[0]的位置不一定是最小的
- for j in range(i):
- if lst[i] < lst[j]:
- lst.insert(j, lst[i])
- # lst[i]已经插入到j的位置了,j之后的元素都往后+1位,所以删除lst[i+1]
- del lst[i + 1]
- return lst
-
- print(insert_sort([1, 5, 55, 4, 5, 1, 3, 4, 5, 8, 62, 7]))
希尔排序
希尔排序是1959年Shell发明的,第一个突破O(n2)的排序算法,是简单插入排序的改进版。它与插入排序的不同之处在于,它会优先比较距离较远的元素。希尔排序又叫缩小增量排序。
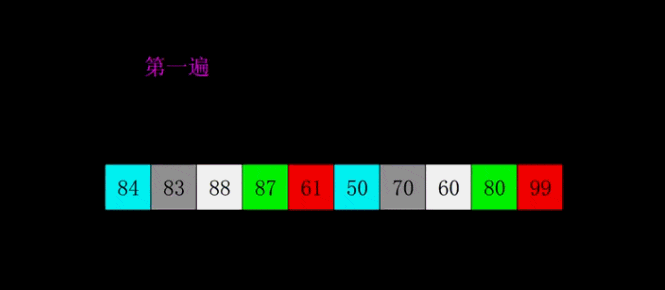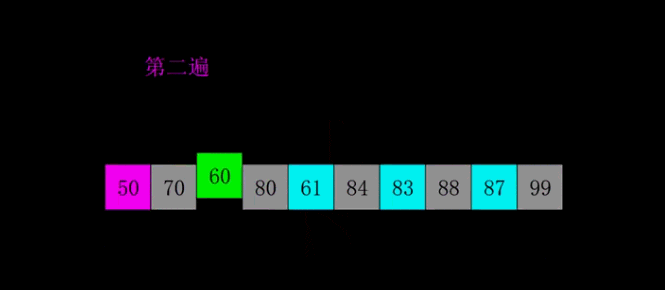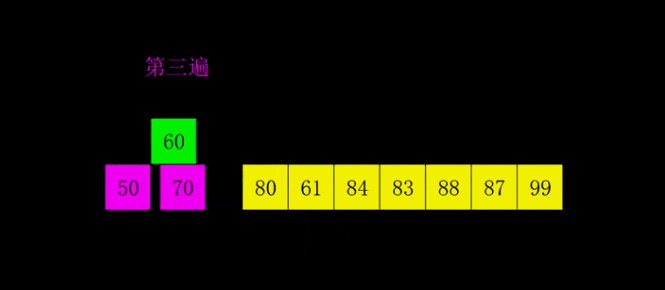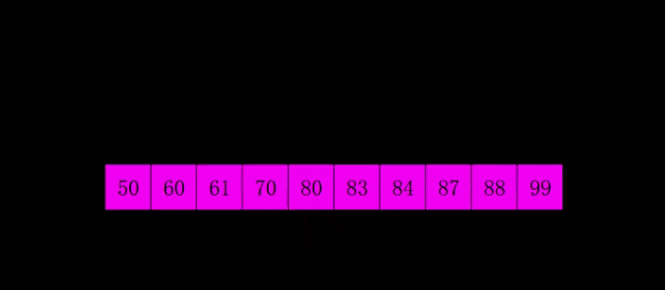
希尔排序
- # 希尔排序是对直接插入排序的优化版本
- # 1. 分组:
- # 每间隔一段距离取一个元素为一组
- # 间隔自己确定,一般为lst的一半
- # 2. 根据插入排序,把每一组排序好
- # 3. 继续分组:
- # 同样没间隔一段距离取一个元素为一组
- # 间隔要求比 之前的间隔少一半
- # 4. 再每组插入排序
- # 5. 直到间隔为1,则排序完成
- #
-
- def shell_sort(lst):
- lst_len = len(lst)
- gap = lst_len // 2 # 整除2,取间隔
- while gap >= 1: # 间隔为0时结束
- for i in range(gap, lst_len):
- temp = lst[i]
- j = i
- # 插入排序
- while j - gap >= 0 and lst[j - gap] > temp:
- lst[j] = lst[j - gap]
- j -= gap
- lst[j] = temp
- gap //= 2
- return lst
-
-
- print(shell_sort([1, 5, 55, 4, 5, 1, 3, 4, 5, 8, 62, 7]))
-
-
- # 奇数
- # gap = 2
- # [5, 2, 4, 3, 1]
- # [5, 4, 1] [2, 3]
- # [1, 4, 5, 2, 3]
- # gap = 1
- # [1, 2, 3, 4, 5]
-
- # 偶数
- # gap = 3
- # [5, 2, 4, 3, 1, 6]
- # [5, 3] [2, 1] [4,6]
- # [3, 5, 1, 2, 4 , 6]
- # gap = 1
- # [1, 2, 3, 4, 5, 6]
并归排序
归并排序是建立在归并操作上的一种有效的排序算法。该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为2-路归并。
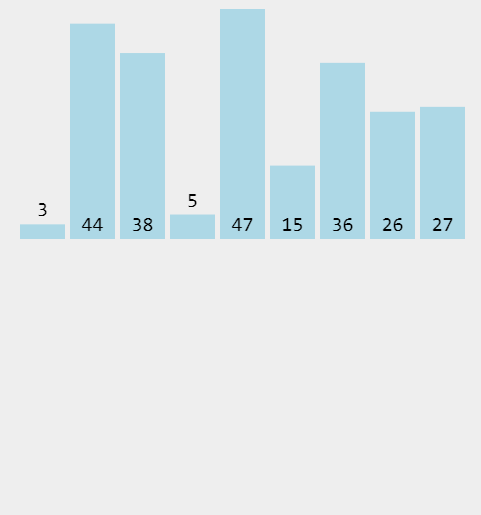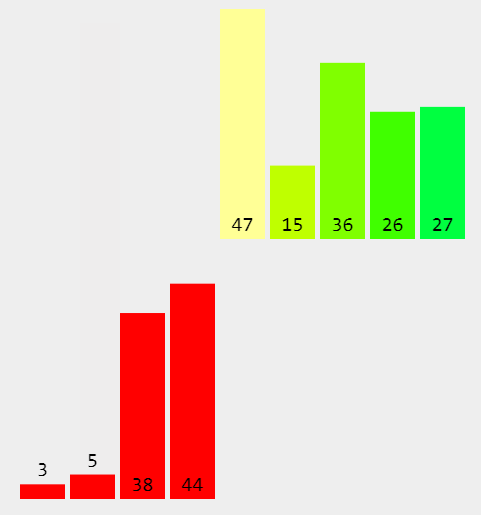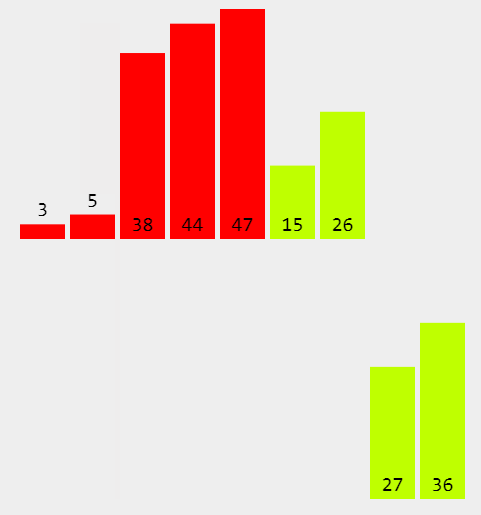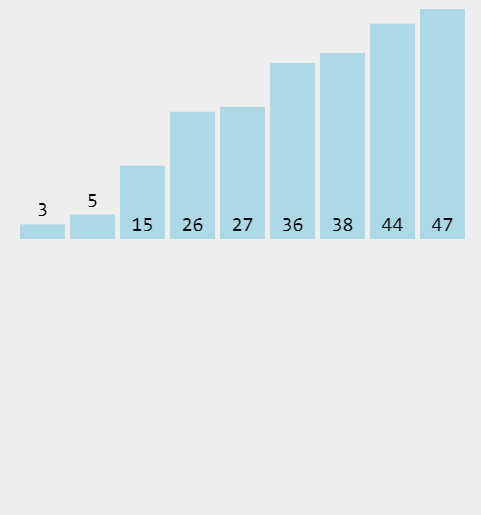
并归排序
- # 利用分治法
- # 不断将lst分为左右两个分
- # 直到不能再分
- # 然后返回
- # 将两边的列表的元素进行比对,排序然后返回
- # 不断重复上面这一步骤
- # 直到排序完成,即两个大的列表比对完成
-
-
- def merge(left, right):
- # left 可能为只有一个元素的列表,或已经排好序的多个元素列表(之前调用过merge)
- # right 也一样
-
- res = []
- while left and right:
- item = left.pop(0) if left[0] < right[0] else right.pop(0)
- res.append(item)
-
- # 此时,left或right已经有一个为空,直接extend插入
- # 而且,left和right是之前已经排好序的列表,不需要再操作了
-
- res.extend(left)
- res.extend(right)
- return res
-
-
- def merge_sort(lst):
- lst_len = len(lst)
- if lst_len <= 1:
- return lst
- mid = lst_len // 2
-
- lst_right = merge_sort(lst[mid:len(lst)]) # 返回的时lst_len <= 1时的 lst 或 merge中进行排序后的列表
- lst_left = merge_sort(lst[:mid]) # 返回的是lst_len <= 1时的 lst 或 merge中进行排序后的列表
-
- return merge(lst_left, lst_right) # 进行排序,lst_left lst_right 的元素会不断增加
-
-
- print(merge_sort([1, 5, 55, 4, 5, 1, 3, 4, 5, 8, 62, 7]))
堆排序
堆排序是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构,并同时满足堆积的性质:即子结点的键值或索引总是小于(或者大于)它的父节点。然后进行排序。

堆排序
- # 把列表创成一个大根堆或小根堆
- # 然后根据大(小)根堆的特点:根节点最大(小),逐一取值
- #
- # 升序----使用大顶堆
- #
- # 降序----使用小顶堆
- # 本例以小根堆为例
- # 列表lst = [1, 22 ,11, 8, 12, 4, 9]
-
- # 1. 建成一个普通的堆:
- # 1
- # / # 22 11
- # / \ / # 8 12 4 9
- #
- # 2. 进行调整,从子开始调整位置,要求: 父节点<= 字节点
- #
- # 1 1 1
- # / \ 13和22调换位置 / \ 4和11调换位置 / # 22 11 ==============> 13 11 ==============> 13 4
- # / \ / \ / \ / \ / \ / # 13 14 4 9 22 14 4 9 22 14 11 9
- #
- # 3. 取出树上根节点,即最小值,把换上叶子节点的最大值
- #
- # 1
- # /
- # ~~~~/
- # 22
- # / # 8 4
- # \ / # 12 11 9
- #
- # 4. 按照同样的道理,继续形成小根堆,然后取出根节点,。。。。重复这个过程
- #
- # 1 1 1 4 1 4 1 4 8 1 4 8
- # / / / / / /
- # ~~~/ ~~~/ ~~~/ ~~~/ ~~~/ ~~~/
- # 22 4 22 8 22 9
- # / \ / \ / \ / \ / \ / # 8 4 8 9 8 9 12 9 12 9 12 11
- # \ / \ \ / \ \ / \ / / /
- # 12 11 9 12 11 22 12 11 22 11 11 22
- #
- # 续上:
- # 1 4 8 9 1 4 8 9 1 4 8 9 11 1 4 8 9 11 1 4 8 9 11 12 ==> 1 4 8 9 11 12 22
- # / / / / /
- # ~~~/ ~~~/ ~~~/ ~~~/ ~~~/
- # 22 11 22 12 22
- # / \ / \ / /
- # 12 11 12 22 12 22
- #
- # 代码实现
-
- def heapify(lst, lst_len, i):
- """创建一个堆"""
- less = i # largest为最大元素的索引
-
- left_node_index = 2 * i + 1 # 左子节点索引
- right_node_index = 2 * i + 2 # 右子节点索引
-
- # lst[i] 就是父节点(假如有子节点的话):
- #
- # lst[i]
- # / # lst[2*i + 1] lst[ 2*i + 2]
- #
-
- # 想要大根堆,即升序, 将判断左右子节点大小的 ‘>' 改为 ‘<' 即可
- #
- if left_node_index < lst_len and lst[less] > lst[left_node_index]:
- less = left_node_index
-
- if right_node_index < lst_len and lst[less] > lst[right_node_index]:
- # 右边节点最小的时候
- less = right_node_index
-
- if less != i:
- # 此时,是字节点大于父节点,所以相互交换位置
- lst[i], lst[less] = lst[less], lst[i] # 交换
- heapify(lst, lst_len, less)
- # 节点变动了,需要再检查一下
-
- def heap_sort(lst):
- res = []
- i = len(lst)
- lst_len = len(lst)
-
- for i in range(lst_len, -1, -1):
- # 要从叶节点开始比较,所以倒着来
- heapify(lst, lst_len, i)
-
- # 此时,已经建好了一个小根树
- # 所以,交换元素,将根节点(最小值)放在后面,重复这个过程
- for j in range(lst_len - 1, 0, -1):
- lst[0], lst[j] = lst[j], lst[0] # 交换,最小的放在j的位置
-
- heapify(lst, j, 0) # 再次构建一个[0: j)小根堆 [j: lst_len-1]已经倒序排好了
- return lst
-
- arr = [1, 5, 55, 4, 5, 1, 3, 4, 5, 8, 62, 7]
- print(heap_sort(arr))
参考:
十大经典排序算法(动图演示)
数据结构与算法-排序篇-Python描述
动图可以点击这里查看
我的github
我的博客
我的笔记
到此这篇关于python3实现常见的排序算法(示例代码)的文章就介绍到这了,更多相关python排序算法内容请搜索w3xue以前的文章或继续浏览下面的相关文章希望大家以后多多支持w3xue!