经验首页 前端设计 程序设计 Java相关 移动开发 数据库/运维 软件/图像 大数据/云计算 其他经验
当前位置：技术经验 » 程序设计 » 编程经验 » 查看文章
平衡树 Treap & Splay [学习笔记]
来源：cnblogs　　作者：lty_ylzsx　　时间：2024/5/27 9:21:18　　对本文有异议

平衡树 \(\tt{Treap}\) & \(\tt{Splay}\)

壹.单旋 \(\tt{Treap}\)

首先了解 \(\tt{BST}\)

非常好用的东西，但是数据可以把它卡成一条链 \(\dots\)

于是，我们将 \(\tt{Tree}\) 与 \(\tt{heap}\) (堆) 合并，以保证平衡树 \(\log\) 的深度。

具体地，我们可以使用旋转操作实现

K8He的图

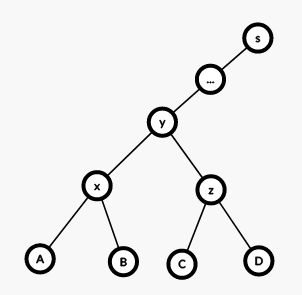
以右旋为例，我们发现，本来的中序遍历顺序为 \(y<p<x<q<z<r\)，那么对于 \(q\) 右旋，即将左儿子旋上来，由于本来 \(p<q\) ，所以显然 \(q\) 要成为 \(p\) 的右儿子。那就剩下 \(x\) 无家可归，我们发现 \(p<x<q\)，那么 \(q\) 的左儿子再适合不过了。

我们规定 \(0\) 方向为左，\(1\) 方向为右，即可通过 \(d\) ^ \(1\) 实现方向取反。

一般的，对于一个节点 \(i\)，如果将其 \(d\) 方向上的儿子 \(s\) 旋上去，那么 \(i\) 要成为 \(s\) 在 \(d\) ^ \(1\) 方向上的儿子，\(s\) 原来在 \(d\) ^ \(1\) 方向上的儿子要成为 \(i\) 在 \(d\) 方向上的儿子。

  1. void rotate(int &i,int d){
  2.     int s=t[i].son[d];
  3.     t[i].son[d]=t[s].son[d^1];
  4.     t[s].son[d^1]=i;
  5.     up(i),i=s,up(i);
  6.     return;
  7. }

那么我们什么时候进行旋转呢？还记得我们说过要利用堆的性质，那么我们对每个节点随机一个优先级，将它按照小根堆或大根堆存，若当前不满足堆的性质了，那就旋转。

  • 插入操作，从根往下跑，但要注意不满足堆的性质时，考虑旋转。
  1. void insert(int &i,int k){
  2.     if(!i){
  3.         i=++tot;
  4.         t[i].cnt=t[i].siz=1;
  5.         t[i].val=k,t[i].rd=rnd();
  6.         return;
  7.     }
  8.     t[i].siz++;
  9.     if(t[i].val==k){
  10.         ++t[i].cnt;return;
  11.     }
  12.     int d=(t[i].val<k);
  13.     insert(t[i].son[d],k);
  14.     if(t[i].rd>t[t[i].son[d]].rd)  rotate(i,d);
  15.     return;
  16. }
  • 删除操作，先找节点，如果只有一个儿子，让儿子替换它，否则让儿子旋上来(当然要满足堆性质)，然后一直旋，直到剩一个儿子或者成为叶子节点。
  1. void del(int &i,int k){
  2.     if(!i)  return;
  3.     if(t[i].val==k){
  4.         if(t[i].cnt>1){
  5.             --t[i].cnt,--t[i].siz;
  6.             return;
  7.         }
  8.         int d=(t[ls(i)].rd>t[rs(i)].rd);
  9.         if(!ls(i)||!rs(i))  i=ls(i)+rs(i);
  10.         else  rotate(i,d),del(i,k);
  11.         return;
  12.     }
  13.     t[i].siz--;
  14.     int d=t[i].val<k;
  15.     del(t[i].son[d],k);
  16.     return;
  17. }
  • 查排名，看代码理解即可。
  1. int rk(int i,int k){
  2.     if(!i) return 1;
  3.     if(t[i].val>k)  return rk(ls(i),k);
  4.     if(t[i].val<k)  return t[ls(i)].siz+t[i].cnt+rk(rs(i),k);
  5.     return t[ls(i)].siz+1;
  6. }
  • 查第 \(k\) 大，思想和线段树一样。
  1. int kth(int i,int k){
  2.     while(1){
  3.         if(k<=t[ls(i)].siz)  i=ls(i);
  4.         else if(k>t[ls(i)].siz+t[i].cnt)
  5.             k-=(t[ls(i)].siz+t[i].cnt),i=rs(i);
  6.         else return t[i].val;
  7.     }
  8. }
  • 前驱后继，和普通 \(\tt{BST}\) 一样。
  1. int pre(int i,int k){
  2.     if(!i)  return -1e8;
  3.     if(t[i].val>=k)  return pre(ls(i),k);
  4.     return max(pre(rs(i),k),t[i].val);
  5. }
  6. int nex(int i,int k){
  7.     if(!i)  return 1e8;
  8.     if(t[i].val<=k)  return nex(rs(i),k);
  9.     return min(nex(ls(i),k),t[i].val);
  10. }

对于单旋 \(\tt{Treap}\)，我们只需要理解旋转操作即可，毕竟下面的 \(\tt{Splay}\) 还要用它，请务必看懂旋转操作，其他的，还是FHQ好打， 差不多看看就行，应用范围不大。

(板子封装在下面题单 普通平衡树 里)

贰.无旋 \(\tt{FHQ\ Treap}\)

由于单旋 \(\tt{Treap}\) 不好打且扩展功能不多，所以我们引入新的 \(\tt{FHQ\_ Treap}\)，好像是神范浩强发明的，%%%%%%。

网上都说FHQ比单旋好理解，我表示理解了之后确实好理解，但你得先理解(我看了一个多小时才看懂，不过我是fw)

好那么直入正题 —— \(\tt{FHQ\_ Treap}\)

既然也是 \(\tt{Treap}\)，那就是一样的，也是靠堆性质，它的不同之处就在于，它无旋，它是靠分裂+合并来保证 \(\log\) 的深度。

具体地，分裂方式有两种，一种是按权值分裂，另一种是按照子树大小分裂:

  • 按照权值分裂，比如将以 \(i\) 为根的平衡树分成两棵平衡树，根分别是 \(x,y\)，要求树 \(x\) 的权值都小于等于 \(k\),剩下是 \(y\)，那么分讨:
    • 如果 \(val(i)<=k\)，那么 \(i\) 的整棵左子树一定都小于 \(k\)，肯定都要划到 \(x\) 里，则令 \(x=i\)，继续递归划分 \(rs(i)\) 即可。
    • 否则，\(i\) 的整棵右子树一定都大于 \(k\)，肯定都要划到 \(y\) 里，则令 \(y=i\)，继续递归划分 \(ls(i)\) 即可。

注意取地址。

  1. void split(int i,int k,int &x,int &y){
  2.     if(!i){x=y=0;return;}
  3.     if(val(i)>k)   y=i,split(ls(i),k,x,ls(i));
  4.     if(val(i)<=k)  x=i,split(rs(i),k,rs(i),y);
  5.     up(i);return;
  6. }
  • 按照子树大小分裂，还是将以 \(i\) 为根的平衡树分成两棵平衡树，根分别是 \(x,y\)，要求是 \(siz(x)=k\)，还是和上面一样:
    • 如果 \(siz(ls(i))+cnt(i)<=k\)，那么 \(i\) 的整棵左子树和 \(i\) 肯定都要划到 \(x\) 里，则令 \(x=i\)，继续递归划分 \(rs(i)\) 即可。
    • 否则，\(i\) 的整棵右子树肯定都要划到 \(y\) 里，则令 \(y=i\)，继续递归划分 \(ls(i)\) 即可。

按子树大小分裂，一般用在平衡树维护序列，后面的 \(\tt{Splay}\) 也是一样。

  1. void split(int i,int k,int &x,int &y){
  2.     if(!i){x=y=0;return;}
  3.     if(siz(ls(i))+cnt(i)<=k)  x=i,split(rs(i),k-(siz(ls(i))+cnt(i)),rs(i),y);
  4.     else  y=i,split(ls(i),k,x,ls(i));
  5.     up(i);
  6. }
  • 下一个操作是合并，\(\tt{FHQ\_ Treap}\) 正是通过它保证的堆性质，设要合并的两棵树的根分别为 \(x,y\)，设堆性质为大根堆。
    • 若 \(rd(x)>rd(y)\) 则把 \(x\) 定为根，然后继续递归合并 \(rs(x)\) 和 \(y\)
    • 否则把 \(y\) 定为根，然后继续递归合并 \(x\) 和 \(ls(y)\)
  1. void merge(int &i,int x,int y){
  2.     if(!x||!y){i=x|y;return;}
  3.     if(rd(x)>rd(y))  merge(rs(x),rs(x),y),i=x;
  4.     else  merge(ls(y),x,ls(y)),i=y;
  5.     up(i);return;
  6. }
  • 插入 \(k\)，先分裂出 \(<=k-1\)，合并时把 \(k\) 合并进去。
  1. void insert(int k){
  2.     int rt1,rt2;
  3.     split(rt,k-1,rt1,rt2);
  4.     merge(rt,rt1,New(k));merge(rt,rt,rt2);
  5.     return;
  6. }
  • 删除 \(k\)，把 \(k\) 分裂出来，然后把 \(k\) 用它的左右子树合并替代，再合并。
  1. void del(int k){
  2.     int rt1,rt2,cut;
  3.     split(rt,k-1,rt1,rt2);split(rt2,k,cut,rt2);
  4.     merge(cut,ls(cut),rs(cut));
  5.     merge(rt,rt1,cut);merge(rt,rt,rt2);
  6.     return;
  7. }
  • 查排名，分裂完 \(\leq k-1\) 的树大小 \(+1\)
  1. int rk(int i,int k){
  2.     int rt1,rt2,res;
  3.     split(i,k-1,rt1,rt2);
  4.     res=siz(rt1)+1;
  5.     merge(i,rt1,rt2);
  6.     return res;
  7. }

  • 第 \(k\) 小，和普通 \(\tt{Treap}\) 一样。

  • 前驱后继，以前驱为例，分裂出 \(\leq k-1\)，那么这部分都小于 \(k\)，找出最大值即可，一直跑右儿子，后继同理。

  1. int pre(int &i,int k){
  2.     int rt1,rt2,res;
  3.     split(i,k-1,rt1,rt2),res=rt1;
  4.     while(rs(res))  res=rs(res);
  5.     merge(i,rt1,rt2);
  6.     return val(res);
  7. }
  8. int nxt(int &i,int k){
  9.     int rt1,rt2,res;
  10.     split(i,k,rt1,rt2),res=rt2;
  11.     while(ls(res))  res=ls(res);
  12.     merge(i,rt1,rt2);
  13.     return val(res);
  14. }

(板子封装在下面题单 普通平衡树 里)

叁.双旋 \(\tt{Splay}\)

\(\tt{Splay}\) 不同于以上两种 \(\tt{Treap}\)，它不再依靠随机的优先级保证深度，而是通过不断旋转来达到目的。

类似于单旋，只不过单旋是将某节点的儿子旋上来，而 \(\tt{Splay}\) 是将某节点自身旋上去，单次旋转和 \(\tt{Treap}\) 一样，但是要多记录一个父亲

具体地，旋转 \(x\) 时，令 \(y\) 为 \(x\) 的父亲，\(z\) 为祖父，设 \(x\) 为 \(y\) 在 \(d\) 方向上的儿子，则单次旋转可分为这几步:

  • \(x\) 替换 \(y\) 成为 \(z\) 的儿子
  • \(x\) 在 \(d\) ^ \(1\) 方向的儿子下放给 \(y\) 当 \(d\) 方向的儿子
  • \(y\) 充当 \(x\) 在 \(d\) ^ \(1\) 方向的儿子

三次修改，三次认爹，rotate就写完了

  1. #define ds(i) t[i].son[d]
  2. #define bs(i) t[i].son[d^1] 
  3. void rotate(int x){
  4.     int y=fa(x),z=fa(y);
  5.     int d=(rs(y)==x);
  6.     t[z].son[(rs(z)==y)]=x;fa(x)=z;
  7.     ds(y)=bs(x);fa(bs(x))=y;
  8.     bs(x)=y;fa(y)=x;
  9.     up(y),up(x);
  10. }

然后便是 \(\tt{Splay}\) 的核心操作，splay 如说

具体地，splay 操作是将节点 \(x\) 旋转到目标节点 \(s\) 的儿子，若 \(s=0\) 则为旋转到根。那么如果我们一直一直单旋上去的话我们会发现一个严重的问题——虽然 \(x\) 上去了，但是它的最大深度依然没变，也就是说，转了个寂寞。。

那么怎么办，进行双旋，讨论几种情况——(\(x,y,z\) 意义同上)

  • \(z=s\) 直接将 \(x\) 单旋一次上去

  • \(z\not ={s}\)

    • \(x,y,z\) 三点共线，即

    此时我们应先转 \(y\) 再转 \(x\)

    -

    • \(x,y,z\) 三点不共线，直接旋转两次 \(x\)

    -

就这样旋旋旋，就能保证深度OK，每次插入节点后都要进行一次 Splay

  1. void splay(int x,int s){
  2.     while(fa(x)!=s){
  3.         int y=fa(x),z=fa(y);
  4.         if(z!=s)
  5.             (ls(y)==x)^(ls(z)==y)?rotate(x):rotate(y);
  6.         rotate(x);
  7.     }
  8.     if(!s)  rt=x;
  9. }

至于这么旋为什么可以让复杂度OK，使用什么"势能分析法"，我是fw我不会。

\(\tt{Splay}\) 与 \(\tt{FHQ}\) 一样，也是两种维护方式，一种维护权值，一种维护下标(即序列的中序遍历)。

然后就是 \(\tt{Splay}\) 的一些基本操作:

  • 插入，有两种方式，即按权值和子树大小，与 \(\tt{FHQ}\) 类似，注意要记录一下父亲节点

    • 按照权值插入
    1. void insert(int k){
    2.     int p=rt,f=0;
    3.     while(p&&val(p)!=k){
    4.         f=p;
    5.         p=t[p].son[val(p)<k];
    6.     }
    7.     if(p)  ++cnt(p);
    8.     else{
    9.         p=++tot;
    10.         if(f)  t[f].son[val(f)<k]=p;
    11.         val(p)=k;fa(p)=f;
    12.         siz(p)=cnt(p)=1;
    13.     }
    14.     splay(p,0);
    15. }
    • 按照子树大小插入，可以递归写(爱咋写咋写)
    1. void insert(int &i,int f,int x,int k){
    2.     if(!i){
    3.         i=++tot;
    4.         siz(i)=1;fa(i)=f;val(i)=k;
    5.         return;
    6.     }
    7.     if(x<=siz(ls(i))+1)  insert(ls(i),i,x,k);
    8.     else  insert(rs(i),i,x-siz(ls(i))-1,k);
    9.     up(i);
    10. }

  • 对于splay，我们要先找到某权值对应的节点，直接找然后splay

    • 权值
    1. void find(int k){
    2.     if(!rt)  return;
    3.     int p=rt;
    4.     while(t[p].son[val(p)<k]&&val(p)!=k){
    5.         p=t[p].son[val(p)<k];
    6.     }
    7.     splay(p,0);
    8. }
    • 子树大小
    1. void find(int x){
    2.     if(!rt)  return;
    3.     int p=rt;
    4.     while(siz(ls(p))+1!=x){
    5.         if(x<=siz(ls(p))+1){
    6.             p=ls(p);
    7.         }
    8.         else{
    9.             x-=(siz(ls(p))+1);
    10.             p=rs(p);
    11.         }
    12.     }
    13.     splay(p,0);
    14. }

  • 查第 \(k\) 小，与 \(\tt{Treap}\) 同理，不再赘述

  • 查排名，转到根节点后左子树的大小 \(+1\) 即可

  • 查前驱后继，以前驱为例，转到根之后左子树里最大值即前驱，后继同理

  • 删除比较有意思，我们先找到前驱后继，然后将前驱splay到根，将后继splay到前驱的右儿子，那么要删除的节点就一定为 \(ls(rs(rt))\) (如下图)。这也就意味着必须有前驱后继，否则删不了，那么直接插入两个极值哨兵节点即可。

  1.      pre
  2.     /     ...   nxt
  3.         /        cut  ...
  1. void del(int k){
  2.     int prek=pre(k);
  3.     int nxtk=nxt(k);
  4.     splay(prek,0);splay(nxtk,prek);
  5.     int cut=ls(nxtk);
  6.     if(cnt(cut)>1)
  7.         --cnt(cut),splay(cut,0);
  8.     else  ls(nxtk)=0;
  9. }

另外，维护序列的 \(\tt{Splay}\) 进行区间操作时，也是将区间转化为子树,和删除操作类似，比如文艺平衡树就是这样，不再赘述。

最后注意一定要插哨兵

(板子封装在下面题单 普通平衡树 里)

肆.\(hs\)题单

\(T_D\) 普通平衡树

由于是纯板子，所以先挂 \(T_D\)。

普通Treap 
  1. #include<bits/stdc++.h>
  2. using namespace std;
  4. #define read read()
  5. #define pt puts("")
  6. inline int read{
  7.     int x=0,f=1;char c=getchar();
  8.     while(c<'0'||c>'9') {if(c=='-')  f=-1;c=getchar();}
  9.     while(c>='0'&&c<='9')   x=(x<<3)+(x<<1)+c-'0',c=getchar();
  10.     return f*x;
  11. }
  12. void write(int x){
  13.     if(x<0)  putchar('-'),x=-x;
  14.     if(x>9)  write(x/10);
  15.     putchar(x%10+'0');
  16.     return;
  17. }
  18. #define N 100010
  19. int m;
  21. namespace TREAP{
  22.     mt19937 rnd(0x7f);
  23.     struct Treap{
  24.         int son[2],cnt,siz,val,rd;
  25.         #define ls(i) t[i].son[0]
  26.         #define rs(i) t[i].son[1]
  27.     }t[N];
  28.     int tot,rt;
  29.     void up(int i){
  30.         t[i].siz=t[ls(i)].siz+t[rs(i)].siz+t[i].cnt;
  31.     }
  32.     void rotate(int &i,int d){
  33.         int s=t[i].son[d];
  34.         t[i].son[d]=t[s].son[d^1];
  35.         t[s].son[d^1]=i;
  36.         up(i),i=s,up(i);
  37.         return;
  38.     }
  39.     void insert(int &i,int k){
  40.         if(!i){
  41.             i=++tot;
  42.             t[i].cnt=t[i].siz=1;
  43.             t[i].val=k,t[i].rd=rnd();
  44.             return;
  45.         }
  46.         t[i].siz++;
  47.         if(t[i].val==k){
  48.             ++t[i].cnt;return;
  49.         }
  50.         int d=(t[i].val<k);
  51.         insert(t[i].son[d],k);
  52.         if(t[i].rd>t[t[i].son[d]].rd)  rotate(i,d);
  53.         return;
  54.     }
  55.     void del(int &i,int k){
  56.         if(!i)  return;
  57.         if(t[i].val==k){
  58.             if(t[i].cnt>1){
  59.                 --t[i].cnt,--t[i].siz;
  60.                 return;
  61.             }
  62.             int d=(t[ls(i)].rd>t[rs(i)].rd);
  63.             if(!ls(i)||!rs(i))  i=ls(i)+rs(i);
  64.             else  rotate(i,d),del(i,k);
  65.             return;
  66.         }
  67.         t[i].siz--;
  68.         int d=t[i].val<k;
  69.         del(t[i].son[d],k);
  70.         return;
  71.     }
  72.     int rk(int i,int k){
  73.         if(!i) return 1;
  74.         if(t[i].val>k)  return rk(ls(i),k);
  75.         if(t[i].val<k)  return t[ls(i)].siz+t[i].cnt+rk(rs(i),k);
  76.         return t[ls(i)].siz+1;
  77.     }
  78.     int kth(int i,int k){
  79.         while(1){
  80.             if(k<=t[ls(i)].siz)  i=ls(i);
  81.             else if(k>t[ls(i)].siz+t[i].cnt)
  82.                 k-=(t[ls(i)].siz+t[i].cnt),i=rs(i);
  83.             else return t[i].val;
  84.         }
  85.     }
  86.     int pre(int i,int k){
  87.         if(!i)  return -1e8;
  88.         if(t[i].val>=k)  return pre(ls(i),k);
  89.         return max(pre(rs(i),k),t[i].val);
  90.     }
  91.     int nex(int i,int k){
  92.         if(!i)  return 1e8;
  93.         if(t[i].val<=k)  return nex(rs(i),k);
  94.         return min(nex(ls(i),k),t[i].val);
  95.     }
  96. } using namespace TREAP;
  98. signed main()
  99. {
  100.     #ifndef ONLINE_JUDGE
  101.         freopen("lty.in","r",stdin);
  102.         freopen("lty.out","w",stdout);
  103.     #endif
  104.     m=read;
  105.     int op,x;
  106.     while(m-->0){
  107.         op=read,x=read;
  108.         switch(op){
  109.             case 1:
  110.                 insert(rt,x);break;
  111.             case 2:
  112.                 del(rt,x);break;
  113.             case 3:
  114.                 write(rk(rt,x));pt;break;
  115.             case 4:
  116.                 write(kth(rt,x));pt;break;
  117.             case 5:
  118.                 write(pre(rt,x));pt;break;
  119.             case 6:
  120.                 write(nex(rt,x));pt;break;
  121.         }
  122.     }
  124.     return 0;
  125. }
FHQ_Treap 
  1. #include<bits/stdc++.h>
  2. using namespace std;
  4. #define read read()
  5. #define pt puts("")
  6. inline int read{
  7.     int x=0,f=1;char c=getchar();
  8.     while(c<'0'||c>'9') {if(c=='-')  f=-1;c=getchar();}
  9.     while(c>='0'&&c<='9')   x=(x<<3)+(x<<1)+c-'0',c=getchar();
  10.     return f*x;
  11. }
  12. void write(int x){
  13.     if(x<0)  putchar('-'),x=-x;
  14.     if(x>9)  write(x/10);
  15.     putchar(x%10+'0');
  16.     return;
  17. }
  18. const int N=1e5+10;
  19. namespace FHQ_TREAP{
  20.     struct Treap{
  21.         int son[2],rd,cnt,siz,val;
  22.         #define ls(i) t[i].son[0]
  23.         #define rs(i) t[i].son[1]
  24.         #define rd(i) t[i].rd
  25.         #define cnt(i) t[i].cnt
  26.         #define siz(i) t[i].siz
  27.         #define val(i) t[i].val
  28.     }t[N];
  29.     int tot,rt;
  30.     void up(int i){
  31.         siz(i)=cnt(i)+siz(ls(i))+siz(rs(i));
  32.     }
  33.     int New(int k){
  34.         val(++tot)=k;
  35.         cnt(tot)=siz(tot)=1;
  36.         rd(tot)=rand();
  37.         return tot;
  38.     }
  39.     void split(int i,int k,int &x,int &y){
  40.         if(!i){x=y=0;return;}
  41.         if(val(i)>k)   y=i,split(ls(i),k,x,ls(i));
  42.         if(val(i)<=k)  x=i,split(rs(i),k,rs(i),y);
  43.         up(i);return;
  44.     }
  45.     void merge(int &i,int x,int y){
  46.         if(!x||!y){i=x|y;return;}
  47.         if(rd(x)>rd(y))  merge(rs(x),rs(x),y),i=x;
  48.         else  merge(ls(y),x,ls(y)),i=y;
  49.         up(i);return;
  50.     }
  51.     void insert(int k){
  52.         int rt1,rt2;
  53.         split(rt,k-1,rt1,rt2);
  54.         merge(rt,rt1,New(k));merge(rt,rt,rt2);
  55.         return;
  56.     }
  57.     void del(int k){
  58.         int rt1,rt2,cut;
  59.         split(rt,k-1,rt1,rt2);split(rt2,k,cut,rt2);
  60.         merge(cut,ls(cut),rs(cut));
  61.         merge(rt,rt1,cut);merge(rt,rt,rt2);
  62.         return;
  63.     }
  64.     int rk(int i,int k){
  65.         int rt1,rt2,res;
  66.         split(i,k-1,rt1,rt2);
  67.         res=siz(rt1)+1;
  68.         merge(i,rt1,rt2);
  69.         return res;
  70.     }
  71.     int kth(int i,int k){
  72.         while(1){
  73.             if(k<=siz(ls(i)))  i=ls(i);
  74.             else if(k>siz(ls(i))+cnt(i))
  75.                 k-=(siz(ls(i))+cnt(i)),i=rs(i);
  76.             else return val(i);
  77.         }
  78.     }
  79.     int pre(int &i,int k){
  80.         int rt1,rt2,res;
  81.         split(i,k-1,rt1,rt2),res=rt1;
  82.         while(rs(res))  res=rs(res);
  83.         merge(i,rt1,rt2);
  84.         return val(res);
  85.     }
  86.     int nxt(int &i,int k){
  87.         int rt1,rt2,res;
  88.         split(i,k,rt1,rt2),res=rt2;
  89.         while(ls(res))  res=ls(res);
  90.         merge(i,rt1,rt2);
  91.         return val(res);
  92.     }
  93. } using namespace FHQ_TREAP;
  94. int m;
  95. signed main()
  96. {
  97.     #ifndef ONLINE_JUDGE
  98.         freopen("lty.in","r",stdin);
  99.         freopen("lty.out","w",stdout);
  100.     #endif
  101.     srand(time(0));
  102.     m=read;
  103.     int op,x;
  104.     while(m-->0){
  105.         op=read,x=read;
  106.         switch(op){
  107.             case 1:
  108.                 insert(x);
  109.                 break;
  110.             case 2:
  111.                 del(x);
  112.                 break;
  113.             case 3:
  114.                 write(rk(rt,x));pt;
  115.                 break;
  116.             case 4:
  117.                 write(kth(rt,x));pt;
  118.                 break;
  119.             case 5:
  120.                 write(pre(rt,x));pt;
  121.                 break;
  122.             case 6:
  123.                 write(nxt(rt,x));pt;
  124.                 break;
  125.             default:break;
  126.         }
  127.     }
  128.     return 0;
  129. }
Splay 
  1. #include<bits/stdc++.h>
  2. using namespace std;
  4. #define read read()
  5. #define pt puts("")
  6. inline int read{
  7.     int x=0,f=1;char c=getchar();
  8.     while(c<'0'||c>'9') {if(c=='-')  f=-1;c=getchar();}
  9.     while(c>='0'&&c<='9')   x=(x<<3)+(x<<1)+c-'0',c=getchar();
  10.     return f*x;
  11. }
  12. void write(int x){
  13.     if(x<0)  putchar('-'),x=-x;
  14.     if(x>9)  write(x/10);
  15.     putchar(x%10+'0');
  16.     return;
  17. }
  18. const int N = 1e5+10;
  19. int n;
  20. namespace SPLAY{
  21.     struct Splay_Tree{
  22.         int son[2],fa,cnt,siz,val;
  23.         #define ls(i) t[i].son[0]
  24.         #define rs(i) t[i].son[1]
  25.         #define ds(i) t[i].son[d]
  26.         #define bs(i) t[i].son[d^1]
  27.         #define fa(i) t[i].fa
  28.         #define cnt(i) t[i].cnt
  29.         #define siz(i) t[i].siz
  30.         #define val(i) t[i].val
  31.     }t[N];
  32.     int tot,rt;
  33.     void up(int i){
  34.         siz(i)=siz(ls(i))+siz(rs(i))+cnt(i);
  35.     }
  36.     void rotate(int x){
  37.         int y=fa(x),z=fa(y);
  38.         int d=(rs(y)==x);
  39.         t[z].son[(rs(z)==y)]=x;fa(x)=z;
  40.         ds(y)=bs(x);fa(bs(x))=y;
  41.         bs(x)=y;fa(y)=x;
  42.         up(y),up(x);
  43.     }
  44.     void splay(int x,int s){
  45.         while(fa(x)!=s){
  46.             int y=fa(x),z=fa(y);
  47.             if(z!=s)
  48.                 (ls(y)==x)^(ls(z)==y)?rotate(x):rotate(y);
  49.             rotate(x);
  50.         }
  51.         if(!s)  rt=x;
  52.     }
  53.     void find(int k){
  54.         if(!rt)  return;
  55.         int p=rt;
  56.         while(t[p].son[val(p)<k]&&val(p)!=k){
  57.             p=t[p].son[val(p)<k];
  58.         }
  59.         splay(p,0);
  60.     }
  61.     void insert(int k){
  62.         int p=rt,f=0;
  63.         while(p&&val(p)!=k){
  64.             f=p;
  65.             p=t[p].son[val(p)<k];
  66.         }
  67.         if(p)  ++cnt(p);
  68.         else{
  69.             p=++tot;
  70.             if(f)  t[f].son[val(f)<k]=p;
  71.             val(p)=k;fa(p)=f;
  72.             siz(p)=cnt(p)=1;
  73.         }
  74.         splay(p,0);
  75.     }
  76.     int pre(int k){
  77.         find(k);int p=rt;
  78.         if(val(p)<k)  return p;
  79.         p=ls(p);while(rs(p))  p=rs(p);
  80.         return p;
  81.     }
  82.     int nxt(int k){
  83.         find(k);int p=rt;
  84.         if(val(p)>k)  return p;
  85.         p=rs(p);while(ls(p))  p=ls(p);
  86.         return p;
  87.     }
  88.     void del(int k){
  89.         int prek=pre(k);
  90.         int nxtk=nxt(k);
  91.         splay(prek,0);splay(nxtk,prek);
  92.         int cut=ls(nxtk);
  93.         if(cnt(cut)>1)
  94.             --cnt(cut),splay(cut,0);
  95.         else  ls(nxtk)=0;
  96.     }
  97.     int kth(int k){
  98.         int i=rt;
  99.         if(siz(i)<k)  return 1;
  100.         while(1){
  101.             if(k<=siz(ls(i)))  i=ls(i);
  102.             else if(k>siz(ls(i))+cnt(i))
  103.                 k-=(siz(ls(i))+cnt(i)),i=rs(i);
  104.             else  return val(i);
  105.         }
  106.     }
  107. } using namespace SPLAY;
  109. signed main()
  110. {
  111.     #ifndef ONLINE_JUDGE
  112.         freopen("lty.in","r",stdin);
  113.         freopen("lty.out","w",stdout);
  114.     #endif
  115.     n=read;
  116.     insert(-1e8);insert(1e8);
  117.     int op,x;
  118.     for(int i=1;i<=n;i++){
  119.         op=read,x=read;
  120.         switch(op){
  121.         case 1:
  122.             insert(x);break;
  123.         case 2:
  124.             del(x);break;
  125.         case 3:
  126.             find(x);
  127.             write(siz(ls(rt))),pt;break;
  128.         case 4:
  129.             write(kth(x+1)),pt;break;
  130.         case 5:
  131.             write(val(pre(x))),pt;break;
  132.         case 6:
  133.             write(val(nxt(x))),pt;break;
  134.         default:
  135.             break;
  136.         }
  137.     }
  139.     return 0;
  140. }

\(T_A\) 营业额统计

板子，求前驱后继。

普通Treap 
  1. #include<bits/stdc++.h>
  2. using namespace std;
  3. #define inf 1e10
  4. #define int long long
  5. #define read read()
  6. #define pt puts("")
  7. inline int read{
  8.     int x=0,f=1;char c=getchar();
  9.     while(c<'0'||c>'9') {if(c=='-')  f=-1;c=getchar();}
  10.     while(c>='0'&&c<='9')   x=(x<<3)+(x<<1)+c-'0',c=getchar();
  11.     return f*x;
  12. }
  13. void write(int x){
  14.     if(x<0)  putchar('-'),x=-x;
  15.     if(x>9)  write(x/10);
  16.     putchar(x%10+'0');
  17.     return;
  18. }
  19. const int N=(1<<15)+10;
  20. int n;
  21. int a;
  22. int ans;
  23. namespace TREAP{
  24.     mt19937 Rand(0x7f);
  25.     int tot,rt;
  26.     struct Treap{
  27.         int son[2],val,rd;
  28.         #define ls(i) t[i].son[0]
  29.         #define rs(i) t[i].son[1]
  30.         #define val(i) t[i].val
  31.         #define rd(i) t[i].rd
  32.     }t[N];
  33.     void rotate(int &i,int d){
  34.         int s=t[i].son[d];
  35.         t[i].son[d]=t[s].son[d^1];
  36.         t[s].son[d^1]=i;
  37.         i=s;
  38.         return;
  39.     }
  40.     void insert(int &i,int k){
  41.         if(!i){
  42.             i=++tot;
  43.             val(i)=k;rd(i)=Rand();
  44.             return;
  45.         }
  46.         if(val(i)==k){
  47.             return;
  48.         }
  49.         int d=(val(i)<k);
  50.         insert(t[i].son[d],k);
  51.         if(rd(i)>rd(t[i].son[d]))  rotate(i,d);
  52.     }
  53.     int pre(int i,int k){
  54.         if(!i)  return -inf;
  55.         if(val(i)>k)  return pre(ls(i),k);
  56.         return max(val(i),pre(rs(i),k));
  57.     }
  58.     int nxt(int i,int k){
  59.         if(!i)  return inf;
  60.         if(val(i)<k)  return nxt(rs(i),k);
  61.         return min(val(i),nxt(ls(i),k));
  62.     }
  63. } using namespace TREAP;
  65. signed main()
  66. {
  67.     #ifndef ONLINE_JUDGE
  68.         freopen("lty.in","r",stdin);
  69.         freopen("lty.out","w",stdout);
  70.     #endif
  71.     n=read;
  72.     a=read;
  73.     ans=a;
  74.     insert(rt,a);
  75.     for(int i=2;i<=n;i++){
  76.         a=read;
  77.         int prea=pre(rt,a);
  78.         int nxta=nxt(rt,a);
  79.         ans+=min(a-prea,nxta-a);
  80.         insert(rt,a);
  81.     }
  82.     write(ans);
  83.     return 0;
  84. }
FHQ_Treap 
  1. #include<bits/stdc++.h>
  2. using namespace std;
  3. #define int long long
  4. #define read read()
  5. #define pt puts("")
  6. inline int read{
  7.     int x=0,f=1;char c=getchar();
  8.     while(c<'0'||c>'9') {if(c=='-')  f=-1;c=getchar();}
  9.     while(c>='0'&&c<='9')   x=(x<<3)+(x<<1)+c-'0',c=getchar();
  10.     return f*x;
  11. }
  12. void write(int x){
  13.     if(x<0)  putchar('-'),x=-x;
  14.     if(x>9)  write(x/10);
  15.     putchar(x%10+'0');
  16.     return;
  17. }
  18. const int N = (1<<15)+10;
  20. namespace FHQ_TREAP{
  21.     mt19937 Rand(0x7f);
  22.     struct Treap{
  23.         int son[2],rd,cnt,siz,val;
  24.         #define ls(i) t[i].son[0]
  25.         #define rs(i) t[i].son[1]
  26.         #define ds(i) t[i].son[d]
  27.         #define rd(i) t[i].rd
  28.         #define cnt(i) t[i].cnt
  29.         #define siz(i) t[i].siz
  30.         #define val(i) t[i].val
  31.     }t[N];
  32.     int tot,rt;
  33.     void up(int i){
  34.         siz(i)=cnt(i)+siz(ls(i))+siz(rs(i));
  35.     }
  36.     int New(int k){
  37.         val(++tot)=k;
  38.         cnt(tot)=siz(tot)=1;
  39.         rd(tot)=Rand();
  40.         return tot;
  41.     }
  42.     void split(int i,int k,int &x,int &y){
  43.         if(!i){x=y=0;return;}
  44.         if(val(i)>k)  y=i,split(ls(i),k,x,ls(i));
  45.         if(val(i)<=k) x=i,split(rs(i),k,rs(i),y);
  46.         up(i);
  47.     }
  48.     void merge(int &i,int x,int y){
  49.         if(!x||!y){i=x|y;return;}
  50.         if(rd(x)>rd(y))  merge(rs(x),rs(x),y),i=x;
  51.         else  merge(ls(y),x,ls(y)),i=y;
  52.         up(i);
  53.     }
  54.     void insert(int k){
  55.         int rt1,rt2;
  56.         split(rt,k-1,rt1,rt2);
  57.         merge(rt,rt1,New(k));
  58.         merge(rt,rt,rt2);
  59.     }
  60.     int pre(int k){
  61.         int rt1,rt2;
  62.         split(rt,k,rt1,rt2);
  63.         if(!siz(rt1))  return -1e8;
  64.         int res=rt1;
  65.         while(rs(res))  res=rs(res);
  66.         merge(rt,rt1,rt2);
  67.         return val(res);
  68.     }
  69.     int nxt(int k){
  70.         int rt1,rt2;
  71.         split(rt,k-1,rt1,rt2);
  72.         if(!siz(rt2))  return 1e8;
  73.         int res=rt2;
  74.         while(ls(res))  res=ls(res);
  75.         merge(rt,rt1,rt2);
  76.         return val(res);
  77.     }
  78. } using namespace FHQ_TREAP;
  79. int n,a;
  80. int ans;
  81. signed main()
  82. {
  83.     #ifndef ONLINE_JUDGE
  84.         freopen("lty.in","r",stdin);
  85.         freopen("lty.out","w",stdout);
  86.     #endif
  87.     n=read;
  88.     a=read;
  89.     insert(a);
  90.     ans=a;
  91.     for(int i=2;i<=n;i++){
  92.         a=read;
  93.         int prea=pre(a);
  94.         int nxta=nxt(a);
  95.         ans+=min(a-prea,nxta-a);
  96.         insert(a);
  97.     }
  98.     write(ans);
  99.     return 0;
  100. }
Splay 
  1. #include<bits/stdc++.h>
  2. using namespace std;
  3. #define read read()
  4. #define pt puts("")
  5. inline int read{
  6.     int x=0,f=1;char c=getchar();
  7.     while(c<'0'||c>'9') {if(c=='-')  f=-1;c=getchar();}
  8.     while(c>='0'&&c<='9')   x=(x<<3)+(x<<1)+c-'0',c=getchar();
  9.     return f*x;
  10. }
  11. void write(int x){
  12.     if(x<0)  putchar('-'),x=-x;
  13.     if(x>9)  write(x/10);
  14.     putchar(x%10+'0');
  15.     return;
  16. }
  17. const int N = 1e5+10;
  18. int n;
  19. namespace SPLAY{
  20.     struct Splay_Tree{
  21.         int son[2],fa,cnt,siz,val;
  22.         #define ls(i) t[i].son[0]
  23.         #define rs(i) t[i].son[1]
  24.         #define ds(i) t[i].son[d]
  25.         #define bs(i) t[i].son[d^1]
  26.         #define fa(i) t[i].fa
  27.         #define cnt(i) t[i].cnt
  28.         #define siz(i) t[i].siz
  29.         #define val(i) t[i].val
  30.     }t[N];
  31.     int tot,rt;
  32.     void up(int i){
  33.         siz(i)=siz(ls(i))+siz(rs(i))+cnt(i);
  34.     }
  35.     void rotate(int x){
  36.         int y=fa(x),z=fa(y);
  37.         int d=(rs(y)==x);
  38.         t[z].son[(rs(z)==y)]=x;fa(x)=z;
  39.         ds(y)=bs(x);fa(bs(x))=y;
  40.         bs(x)=y;fa(y)=x;
  41.         up(y),up(x);
  42.     }
  43.     void splay(int x,int s){
  44.         while(fa(x)!=s){
  45.             int y=fa(x),z=fa(y);
  46.             if(z!=s)
  47.                 (ls(y)==x)^(ls(z)==y)?rotate(x):rotate(y);
  48.             rotate(x);
  49.         }
  50.         if(!s)  rt=x;
  51.     }
  52.     void find(int k){
  53.         if(!rt)  return;
  54.         int p=rt;
  55.         while(t[p].son[val(p)<k]&&val(p)!=k){
  56.             p=t[p].son[val(p)<k];
  57.         }
  58.         splay(p,0);
  59.     }
  60.     void insert(int k){
  61.         int p=rt,f=0;
  62.         while(p&&val(p)!=k){
  63.             f=p;
  64.             p=t[p].son[val(p)<k];
  65.         }
  66.         if(p)  ++cnt(p);
  67.         else{
  68.             p=++tot;
  69.             if(f)  t[f].son[val(f)<k]=p;
  70.             val(p)=k;fa(p)=f;
  71.             siz(p)=cnt(p)=1;
  72.         }
  73.         splay(p,0);
  74.     }
  75.     int pre(int k){
  76.         find(k);int p=rt;
  77.         if(val(p)<=k)  return p;
  78.         p=ls(p);while(rs(p))  p=rs(p);
  79.         return p;
  80.     }
  81.     int nxt(int k){
  82.         find(k);int p=rt;
  83.         if(val(p)>=k)  return p;
  84.         p=rs(p);while(ls(p))  p=ls(p);
  85.         return p;
  86.     }
  87. } using namespace SPLAY;
  88. int a,ans;
  89. signed main()
  90. {
  91.     #ifndef ONLINE_JUDGE
  92.         freopen("lty.in","r",stdin);
  93.         freopen("lty.out","w",stdout);
  94.     #endif
  95.     n=read;
  96.     insert(-1e8);insert(1e8);
  97.     a=read;
  98.     ans=a;
  99.     insert(a);
  100.     for(int i=2;i<=n;i++){
  101.         a=read;
  102.         int prea=val(pre(a)),nxta=val(nxt(a));
  103.         ans+=min(a-prea,nxta-a);
  104.         insert(a);
  105.     }
  106.     write(ans);
  108.     return 0;
  109. }

\(T_B\) 宠物收养所

发现某时刻的平衡树里只会全是人或者全是狗，查前驱后继即可，查完即删。

普通Treap 
  1. #include<bits/stdc++.h>
  2. using namespace std;
  3. #define int long long
  4. #define inf 1e10
  5. #define read read()
  6. #define pt puts("")
  7. inline int read{
  8.     int x=0,f=1;char c=getchar();
  9.     while(c<'0'||c>'9') {if(c=='-')  f=-1;c=getchar();}
  10.     while(c>='0'&&c<='9')   x=(x<<3)+(x<<1)+c-'0',c=getchar();
  11.     return f*x;
  12. }
  13. void write(int x){
  14.     if(x<0)  putchar('-'),x=-x;
  15.     if(x>9)  write(x/10);
  16.     putchar(x%10+'0');
  17.     return;
  18. }
  19. const int N=8*1e4+10;
  20. const int p=1e6;
  21. int n;
  22. namespace TREAP{
  23.     mt19937 Rand(0x7f);
  24.     struct Treap{
  25.         int son[2],cnt,siz,val,rd;
  26.         #define ls(i) t[i].son[0]
  27.         #define rs(i) t[i].son[1]
  28.         #define cnt(i) t[i].cnt
  29.         #define siz(i) t[i].siz
  30.         #define val(i) t[i].val
  31.         #define rd(i) t[i].rd
  32.     }t[N];
  33.     int tot,rt;
  34.     void up(int i){
  35.         siz(i)=siz(ls(i))+siz(rs(i))+cnt(i);
  36.     }
  37.     void rotate(int &i,int d){
  38.         int s=t[i].son[d];
  39.         t[i].son[d]=t[s].son[d^1];
  40.         t[s].son[d^1]=i;
  41.         up(i),i=s,up(i);
  42.         return;
  43.     }
  44.     void insert(int &i,int k){
  45.         if(!i){
  46.             i=++tot;
  47.             cnt(i)=siz(i)=1;
  48.             val(i)=k;rd(i)=Rand();
  49.             return;
  50.         }
  51.         siz(i)++;
  52.         if(val(i)==k){
  53.             cnt(i)++;return;
  54.         }
  55.         int d=(val(i)<k);
  56.         insert(t[i].son[d],k);
  57.         if(rd(i)>rd(t[i].son[d]))  rotate(i,d);
  58.         return;
  59.     }
  60.     void del(int &i,int k){
  61.         if(!i)  return;
  62.         if(val(i)==k){
  63.             if(cnt(i)>1){
  64.                 --cnt(i),--siz(i);
  65.                 return;
  66.             }
  67.             int d=(rd(ls(i))>rd(rs(i)));
  68.             if(!ls(i)||!rs(i))  i=ls(i)+rs(i);
  69.             else  rotate(i,d),del(i,k);
  70.             return;
  71.         }
  72.         int d=(val(i)<k);
  73.         --siz(i);
  74.         del(t[i].son[d],k);
  75.         return;
  76.     }
  77.     int pre(int i,int k){
  78.         if(!i)  return -inf;
  79.         if(val(i)>k)  return pre(ls(i),k);
  80.         return max(val(i),pre(rs(i),k));
  81.     }
  82.     int nxt(int i,int k){
  83.         if(!i)  return inf;
  84.         if(val(i)<k)  return nxt(rs(i),k);
  85.         return min(val(i),nxt(ls(i),k));
  86.     }
  87. } using namespace TREAP;
  89. int num[2];
  90. bool now,a;
  91. int b;
  92. int ans;
  93. signed main()
  94. {
  95.     #ifndef ONLINE_JUDGE
  96.         freopen("lty.in","r",stdin);
  97.         freopen("lty.out","w",stdout);
  98.     #endif
  99.     n=read;
  100.     now=read;
  101.     num[now]++;
  102.     b=read;insert(rt,b);
  103.     for(int i=2;i<=n;i++){
  104.         a=read,b=read;
  105.         if(!num[a^1]){
  106.             num[a]++;insert(rt,b);
  107.             now=a;
  108.             continue;
  109.         }
  110.         if(now^a){
  111.             int preb=pre(rt,b);
  112.             int nxtb=nxt(rt,b);
  113.             int hwr=(b-preb<=nxtb-b?preb:nxtb);
  114.             ans=(ans+abs(hwr-b))%p;
  115.             del(rt,hwr);
  116.             --num[now];
  117.         }
  118.         else
  119.             insert(rt,b),++num[now];
  120.     }
  121.     write(ans);
  122.     return 0;
  123. }
Splay 
  1. #include<bits/stdc++.h>
  2. using namespace std;
  3. #define int long long
  4. #define inf 1e10
  5. #define read read()
  6. #define pt puts("")
  7. inline int read{
  8.     int x=0,f=1;char c=getchar();
  9.     while(c<'0'||c>'9') {if(c=='-')  f=-1;c=getchar();}
  10.     while(c>='0'&&c<='9')   x=(x<<3)+(x<<1)+c-'0',c=getchar();
  11.     return f*x;
  12. }
  13. void write(int x){
  14.     if(x<0)  putchar('-'),x=-x;
  15.     if(x>9)  write(x/10);
  16.     putchar(x%10+'0');
  17.     return;
  18. }
  19. const int N = 8*1e4+10;
  20. const int p = 1e6;
  21. int n;
  23. namespace SPLAY{
  24.     struct Splay_Tree{
  25.         int son[2],fa,cnt,siz,val;
  26.         #define ls(i) t[i].son[0]
  27.         #define rs(i) t[i].son[1]
  28.         #define ds(i) t[i].son[d]
  29.         #define bs(i) t[i].son[d^1]
  30.         #define fa(i) t[i].fa
  31.         #define cnt(i) t[i].cnt
  32.         #define siz(i) t[i].siz
  33.         #define val(i) t[i].val
  34.     }t[N];
  35.     int tot,rt;
  36.     void up(int i){
  37.         siz(i)=siz(ls(i))+siz(rs(i))+cnt(i);
  38.     }
  39.     void rotate(int x){
  40.         int y=fa(x),z=fa(y);
  41.         int d=(rs(y)==x);
  42.         t[z].son[(rs(z)==y)]=x;fa(x)=z;
  43.         ds(y)=bs(x);fa(bs(x))=y;
  44.         bs(x)=y;fa(y)=x;
  45.         up(y),up(x);
  46.     }
  47.     void splay(int x,int s){
  48.         while(fa(x)!=s){
  49.             int y=fa(x),z=fa(y);
  50.             if(z!=s)
  51.                 (ls(y)==x)^(ls(z)==y)?rotate(x):rotate(y);
  52.             rotate(x);
  53.         }
  54.         if(!s)  rt=x;
  55.     }
  56.     void insert(int k){
  57.         int p=rt,f=0;
  58.         while(p && val(p)!=k){
  59.             f=p;
  60.             p=t[p].son[val(p)<k];
  61.         }
  62.         if(p)  ++cnt(p);
  63.         else{
  64.             p=++tot;
  65.             if(f)  t[f].son[val(f)<k]=p;
  66.             val(p)=k;fa(p)=f;
  67.             siz(p)=cnt(p)=1;
  68.         }
  69.         splay(p,0);
  70.     }
  71.     void find(int k){
  72.         if(!rt)  return;
  73.         int p=rt;
  74.         while(t[p].son[val(p)<k] && val(p)!=k){
  75.             p=t[p].son[val(p)<k];
  76.         }
  77.         splay(p,0);
  78.     }
  79.     int pre(int k,bool b){
  80.         find(k);int p=rt;
  81.         if(val(p)==k&&b)  return p;
  82.         if(val(p)<k)  return p;
  83.         p=ls(p);while(rs(p))  p=rs(p);
  84.         return p;
  85.     }
  86.     int nxt(int k,bool b){
  87.         find(k);int p=rt;
  88.         if(val(p)==k&&b)  return p;
  89.         if(val(p)>k)  return p;
  90.         p=rs(p);while(ls(p))  p=ls(p);
  91.         return p;
  92.     }
  93.     void del(int k){
  94.         int prek=pre(k,0),nxtk=nxt(k,0);
  95.         splay(prek,0);splay(nxtk,prek);
  96.         int cut=ls(nxtk);
  97.         if(cnt(cut)>1)  --cnt(cut),splay(cut,0);
  98.         else  ls(nxtk)=0;
  99.     }
  100. } 
  101. using namespace SPLAY;
  102. bool now;
  103. int num[2];
  104. int a,b;
  105. int ans;
  106. signed main()
  107. {
  108.     #ifndef ONLINE_JUDGE
  109.         freopen("lty.in","r",stdin);
  110.         freopen("lty.out","w",stdout);
  111.     #endif
  112.     insert(-inf);insert(inf);
  113.     n=read;
  114.     now=read;b=read;num[now]=1;
  115.     insert(b);
  116.     for(int i=2;i<=n;i++){
  117.         a=read,b=read;
  118.         if(!num[a^1]){
  119.             ++num[a],now=a;
  120.             insert(b);
  121.             continue;
  122.         }
  123.         if(a==now){
  124.             ++num[now];
  125.             insert(b);
  126.         }
  127.         else{
  128.             int preb=val(pre(b,1)),nxtb=val(nxt(b,1));
  129.             int hwr=(b-preb<=nxtb-b?preb:nxtb);
  130.             ans=(ans+abs(hwr-b))%p;
  131.             del(hwr);
  132.             --num[now];
  133.         }
  134.     }
  135.     write(ans);
  136.     return 0;
  137. }

注意 \(Splay\) 求前驱后继时如果要取等注意特判，删除时不可取等(取等就寄了)

\(T_C\) 郁闷的出纳员

维护整体懒标记，每次删除低于 \(minn-add\) 线的。

  • 用普通 \(\tt{Treap}\) 直接暴力删，不好打。
  • 用 \(\tt{FHQ\_ Treap}\) 分裂出低于 \(minn-add\) 的部分，直接不要即可。

服了，\(\tt{FHQ\_ Treap}\) 跑不过普通 \(\tt{Treap}\) 的暴力。。。

普通Treap 
  1. #include<bits/stdc++.h>
  2. using namespace std;
  4. #define read read()
  5. #define pt puts("")
  6. inline int read{
  7.     int x=0,f=1;char c=getchar();
  8.     while(c<'0'||c>'9') {if(c=='-')  f=-1;c=getchar();}
  9.     while(c>='0'&&c<='9')   x=(x<<3)+(x<<1)+c-'0',c=getchar();
  10.     return f*x;
  11. }
  12. void write(int x){
  13.     if(x<0)  putchar('-'),x=-x;
  14.     if(x>9)  write(x/10);
  15.     putchar(x%10+'0');
  16.     return;
  17. }
  18. const int N = 1e6;
  19. int n,minn;
  20. int add;
  21. int ans,sum;
  22. int num;
  23. namespace TREAP{
  24.     mt19937 rnd(0x7f);
  25.     struct Treap{
  26.         int son[2],cnt,siz,val,rd;
  27.         #define ls(i) t[i].son[0]
  28.         #define rs(i) t[i].son[1]
  29.         #define val(i) t[i].val
  30.         #define cnt(i) t[i].cnt
  31.         #define siz(i) t[i].siz
  32.     }t[N];
  33.     int tot,rt;
  34.     void up(int i){
  35.         t[i].siz=t[ls(i)].siz+t[rs(i)].siz+t[i].cnt;
  36.     }
  37.     void rotate(int &i,int d){
  38.         int s=t[i].son[d];
  39.         t[i].son[d]=t[s].son[d^1];
  40.         t[s].son[d^1]=i;
  41.         up(i),i=s,up(i);
  42.         return;
  43.     }
  44.     void insert(int &i,int k){
  45.         if(!i){
  46.             i=++tot;
  47.             t[i].cnt=t[i].siz=1;
  48.             t[i].val=k,t[i].rd=rnd();
  49.             return;
  50.         }
  51.         t[i].siz++;
  52.         if(t[i].val==k){
  53.             ++t[i].cnt;return;
  54.         }
  55.         int d=(t[i].val<k);
  56.         insert(t[i].son[d],k);
  57.         if(t[i].rd>t[t[i].son[d]].rd)  rotate(i,d);
  58.         return;
  59.     }
  60.     void del(int &i,int k){
  61.         if(!i)  return;
  62.         if(t[i].val==k){
  63.             if(t[i].cnt>1){
  64.                 --t[i].cnt,--t[i].siz;
  65.                 return;
  66.             }
  67.             int d=(t[ls(i)].rd>t[rs(i)].rd);
  68.             if(!ls(i)||!rs(i))  i=ls(i)+rs(i);
  69.             else  rotate(i,d),del(i,k);
  70.             return;
  71.         }
  72.         t[i].siz--;
  73.         int d=(t[i].val<k);
  74.         del(t[i].son[d],k);
  75.         return;
  76.     }
  77.     int rk(int i,int k){
  78.         if(!i) return 0;
  79.         if(t[i].val>k)  return rk(ls(i),k);
  80.         if(t[i].val<k)  return t[ls(i)].siz+t[i].cnt+rk(rs(i),k);
  81.         return t[ls(i)].siz+1;
  82.     }
  83.     int find(int i,int k){
  84.         while(1){
  85.             if(k<=t[ls(i)].siz)  i=ls(i);
  86.             else if(k>t[ls(i)].siz+t[i].cnt)
  87.                 k-=(t[ls(i)].siz+t[i].cnt),i=rs(i);
  88.             else return t[i].val;
  89.         }
  90.     }
  91.     void dfs(int x){
  92.         if(ls(x))  dfs(ls(x));
  93.         if(rs(x))  dfs(rs(x));
  94.         if(minn-add>val(x)){
  95.             int c=cnt(x);
  96.             for(int i=1;i<=c;i++)
  97.                 del(rt,val(x));
  98.         }
  99.     }
  101. } using namespace TREAP;
  103. signed main()
  104. {
  105.     #ifndef ONLINE_JUDGE
  106.         freopen("lty.in","r",stdin);
  107.         freopen("lty.out","w",stdout);
  108.     #endif
  109.     n=read,minn=read;
  110.     char op;
  111.     int k;
  112.     for(int i=1;i<=n;i++){
  113.         cin>>op;k=read;
  114.         switch (op){
  115.             case 'I':
  116.                 if(k>=minn)  insert(rt,k-add),++num; 
  117.                 break;
  118.             case 'A':
  119.                 add+=k;
  120.                 break;
  121.             case 'S':
  122.                 add-=k;
  123.                 dfs(rt);
  124.                 break;
  125.             case 'F':
  126.                 if(siz(rt)<k)  ans=-1;
  127.                 else ans=find(rt,siz(rt)-k+1)+add;
  128.                 write(ans);pt;
  129.                 break;
  130.             default:
  131.                 break;
  132.         }
  133.     }
  134.     write(num-siz(rt));
  135.     return 0;
  136. }
FHQ_Treap 
  1. #include<bits/stdc++.h>
  2. using namespace std;
  4. #define read read()
  5. #define pt puts("")
  6. inline int read{
  7.     int x=0,f=1;char c=getchar();
  8.     while(c<'0'||c>'9') {if(c=='-')  f=-1;c=getchar();}
  9.     while(c>='0'&&c<='9')   x=(x<<3)+(x<<1)+c-'0',c=getchar();
  10.     return f*x;
  11. }
  12. void write(int x){
  13.     if(x<0)  putchar('-'),x=-x;
  14.     if(x>9)  write(x/10);
  15.     putchar(x%10+'0');
  16.     return;
  17. }
  18. const int N = 1e5+10;
  19. int n,minn,add;
  21. namespace FHQ_TREAP{
  22.     mt19937 Rand(0x7f);
  23.     struct Treap{
  24.         int son[2],rd,cnt,siz,val;
  25.         #define ls(i) t[i].son[0]
  26.         #define rs(i) t[i].son[1]
  27.         #define ds(i) t[i].son[d]
  28.         #define rd(i) t[i].rd
  29.         #define cnt(i) t[i].cnt
  30.         #define siz(i) t[i].siz
  31.         #define val(i) t[i].val
  32.     }t[N];
  33.     int tot,rt;
  34.     void up(int i){
  35.         siz(i)=siz(ls(i))+siz(rs(i))+cnt(i);
  36.     }
  37.     int New(int k){
  38.         val(++tot)=k;
  39.         siz(tot)=cnt(tot)=1;
  40.         rd(tot)=Rand();
  41.         return tot;
  42.     }
  43.     void spilt(int i,int k,int &x,int &y){
  44.         if(!i){x=y=0;return;}
  45.         if(val(i)>k)  y=i,spilt(ls(i),k,x,ls(i));
  46.         if(val(i)<=k) x=i,spilt(rs(i),k,rs(i),y);
  47.         up(i);
  48.     }
  49.     void merge(int &i,int x,int y){
  50.         if(!x||!y){i=x|y;return;}
  51.         if(rd(x)>rd(y))  merge(rs(x),rs(x),y),i=x;
  52.         else  merge(ls(y),x,ls(y)),i=y;
  53.         up(i);
  54.     }
  55.     void insert(int k){
  56.         int rt1,rt2;
  57.         spilt(rt,k-1,rt1,rt2);
  58.         merge(rt,rt1,New(k));
  59.         merge(rt,rt,rt2);
  60.         return;
  61.     }
  62.     void del(int k){
  63.         int rt1,rt2;
  64.         spilt(rt,k-1,rt1,rt2);
  65.         rt=rt2;
  66.     }
  67.     int kth(int i,int k){
  68.         while(1){
  69.             if(k<=siz(ls(i)))  i=ls(i);
  70.             else if(k>siz(ls(i))+cnt(i))
  71.                 k-=(siz(ls(i))+cnt(i)),i=rs(i);
  72.             else return val(i);
  73.         }
  74.     }
  75. } using namespace FHQ_TREAP;
  77. int sum,ans;
  78. signed main()
  79. {
  80.     #ifndef ONLINE_JUDGE
  81.         freopen("lty.in","r",stdin);
  82.         freopen("lty.out","w",stdout);
  83.     #endif
  84.     n=read,minn=read;
  85.     char op;
  86.     int k;
  87.     for(int i=1;i<=n;i++){
  88.         cin>>op;k=read;
  89.         switch(op){
  90.             case 'I':
  91.                 if(k>=minn)
  92.                     insert(k-add),++sum;
  93.                 break;
  94.             case 'A':
  95.                 add+=k;
  96.                 break;
  97.             case 'S':
  98.                 add-=k;
  99.                 del(minn-add);
  100.                 break;
  101.             case 'F':
  102.                 if(siz(rt)<k)  ans=-1;
  103.                 else  ans=kth(rt,siz(rt)-k+1)+add;
  104.                 write(ans);pt;
  105.                 break;
  106.         }
  107.     }
  108.     write(sum-siz(rt));
  109.     return 0;
  110. }

\(T_E\) 文艺平衡树

平衡树不仅具有二叉搜索树的功能，同样可以支持区间操作，即，将序列的下标塞进平衡树，它的中序遍历就是原序列，然后我们想干嘛就干嘛~

对于区间翻转，考虑维护懒标记，下放时交换左右儿子，分别异或。最后中序遍历输出每个节点的值。

对于打懒标记，分裂出 \([l,r]\) 部分，一定要先分出前 \(r\) 个，再分前 \(l-1\) 个，反过来如果先分前 \(l-1\) 个，后面就应该分出 \(r-l+1\) 个，手画一下就知道为什么了。

这里使用 \(\tt{FHQ\_ Treap}\) 时，我们按子树大小进行分裂，因为我们是按照下标建的树，不能按权值分裂。

FHQ_Treap 
  1. #include<bits/stdc++.h>
  2. using namespace std;
  3. #define swap(x,y) (x^=y,y^=x,x^=y)
  4. #define read read()
  5. #define pt puts("")
  6. inline int read{
  7.     int x=0,f=1;char c=getchar();
  8.     while(c<'0'||c>'9') {if(c=='-')  f=-1;c=getchar();}
  9.     while(c>='0'&&c<='9')   x=(x<<3)+(x<<1)+c-'0',c=getchar();
  10.     return f*x;
  11. }
  12. void write(int x){
  13.     if(x<0)  putchar('-'),x=-x;
  14.     if(x>9)  write(x/10);
  15.     putchar(x%10+'0');
  16.     return;
  17. }
  18. const int N = 1e5+10;
  19. int n,m;
  21. namespace FHQ_TREAP{
  22.     struct Treap{
  23.         int son[2],val,cnt,siz,rd,lazy;
  24.         #define ls(i) t[i].son[0]
  25.         #define rs(i) t[i].son[1]
  26.         #define rd(i) t[i].rd
  27.         #define cnt(i) t[i].cnt
  28.         #define siz(i) t[i].siz
  29.         #define val(i) t[i].val
  30.         #define lazy(i) t[i].lazy
  31.     }t[N];
  32.     int tot,rt;
  33.     int New(int k){
  34.         val(++tot)=k;
  35.         cnt(tot)=siz(tot)=1;
  36.         rd(tot)=rand();
  37.         return tot;
  38.     }
  39.     void up(int i){
  40.         siz(i)=siz(ls(i))+siz(rs(i))+cnt(i);
  41.     }
  42.     void down(int i){
  43.         if(!lazy(i))  return;
  44.         swap(ls(i),rs(i));
  45.         lazy(ls(i))^=1;
  46.         lazy(rs(i))^=1;
  47.         lazy(i)=0;
  48.     }
  49.     void split(int i,int k,int &x,int &y){
  50.         if(!i){x=y=0;return;}
  51.         down(i);
  52.         if(siz(ls(i))+cnt(i)<=k)  x=i,split(rs(i),k-(siz(ls(i))+cnt(i)),rs(i),y);
  53.         else  y=i,split(ls(i),k,x,ls(i));
  54.         up(i);
  55.     }
  56.     void merge(int &i,int x,int y){
  57.         if(!x||!y){i=x|y;return;}
  58.         if(rd(x)>rd(y))  down(x),merge(rs(x),rs(x),y),i=x;
  59.         else  down(y),merge(ls(y),x,ls(y)),i=y;
  60.         up(i);
  61.     }
  62.     void insert(int k){
  63.         int rt1,rt2;
  64.         split(rt,k,rt1,rt2);
  65.         merge(rt,rt1,New(k));
  66.         merge(rt,rt,rt2);
  67.     }
  68.     void out(int i){
  69.         down(i);
  70.         if(ls(i))  out(ls(i));
  71.         write(val(i));putchar(' ');
  72.         if(rs(i))  out(rs(i));
  73.     }
  74. } using namespace FHQ_TREAP;
  76. signed main()
  77. {
  78.     #ifndef ONLINE_JUDGE
  79.         freopen("lty.in","r",stdin);
  80.         freopen("lty.out","w",stdout);
  81.     #endif
  82.     srand(time(0));
  83.     n=read,m=read;
  84.     for(int i=1;i<=n;i++)  insert(i);
  85.     int l,r,rt1,rt2,rt3;
  86.     for(int i=1;i<=m;i++){
  87.         l=read,r=read;
  88.         rt1=rt2=rt3=0;
  89.         split(rt,r,rt1,rt3);
  90.         split(rt1,l-1,rt1,rt2);
  91.         lazy(rt2)^=1;
  92.         merge(rt1,rt1,rt2);
  93.         merge(rt,rt1,rt3);
  94.         // split(rt,l-1,rt1,rt2);
  95.         // split(rt2,r-l+1,rt2,rt3);
  96.         // lazy(rt2)^=1;
  97.         // merge(rt2,rt2,rt3);
  98.         // merge(rt,rt1,rt2);
  99.     }
  100.     out(rt);
  101.     return 0;
  102. }

对于 \(\tt{Splay}\)，其实是差不多的，我们都是将区间转到一棵子树上进行打标记，类似于删除操作，我们将 \(l-1\) 转到根，将 \(r+1\) 转到根的儿子，那么 \(ls(rs(rt))\) 的子树就是区间 \([l,r]\)，然后和 \(\tt{FHQ}\) 一样。

我的代码比较排斥 \(0\)，所以我干脆将整体 \(+1\)，最后答案 \(-1\) 输出。

Splay 
  1. #include<bits/stdc++.h>
  2. using namespace std;
  3. #define swap(x,y) (x^=y,y^=x,x^=y)
  4. #define read read()
  5. #define pt puts("")
  6. inline int read{
  7.     int x=0,f=1;char c=getchar();
  8.     while(c<'0'||c>'9') {if(c=='-')  f=-1;c=getchar();}
  9.     while(c>='0'&&c<='9')   x=(x<<3)+(x<<1)+c-'0',c=getchar();
  10.     return f*x;
  11. }
  12. void write(int x){
  13.     if(x<0)  putchar('-'),x=-x;
  14.     if(x>9)  write(x/10);
  15.     putchar(x%10+'0');
  16.     return;
  17. }
  18. const int N = 1e5+10;
  19. int n,m;
  21. namespace SPLAY{
  22.     struct Splay_Tree{
  23.         int son[2],fa,lazy,siz,val;
  24.         #define ls(i) t[i].son[0]
  25.         #define rs(i) t[i].son[1]
  26.         #define ds(i) t[i].son[d]
  27.         #define bs(i) t[i].son[d^1]
  28.         #define fa(i) t[i].fa
  29.         #define lazy(i) t[i].lazy
  30.         #define siz(i) t[i].siz
  31.         #define val(i) t[i].val
  32.     }t[N];
  33.     int tot,rt;
  34.     void up(int i){
  35.         siz(i)=siz(ls(i))+siz(rs(i))+1;
  36.     }
  37.     void down(int i){
  38.         if(!lazy(i))  return;
  39.         lazy(i)=0;
  40.         swap(ls(i),rs(i));
  41.         lazy(ls(i))^=1,lazy(rs(i))^=1;
  42.     }
  43.     void rotate(int x){
  44.         int y=fa(x),z=fa(y);
  45.         int d=(rs(y)==x);
  46.         t[z].son[rs(z)==y]=x;fa(x)=z;
  47.         ds(y)=bs(x);fa(bs(x))=y;
  48.         bs(x)=y;fa(y)=x;
  49.         up(y),up(x);
  50.     }
  51.     void splay(int x,int s){
  52.         while(fa(x)!=s){
  53.             down(x);
  54.             int y=fa(x),z=fa(y);
  55.             if(z!=s)
  56.                 (ls(y)==x)^(ls(z)==y)?rotate(x):rotate(y);
  57.             rotate(x);
  58.         }
  59.         if(!s)  rt=x;
  60.     }
  61.     int find(int k){
  62.         if(!rt)  return 0;
  63.         int p=rt;
  64.         while(siz(ls(p))+1!=k){
  65.             if(k<=siz(ls(p)))
  66.                 p=ls(p);
  67.             else{
  68.                 k-=(siz(ls(p))+1);
  69.                 p=rs(p);
  70.             }
  71.             down(p);
  72.         }
  73.         return p;
  74.     }
  75.     void insert(int &i,int f,int x,int k){
  76.         if(!i){
  77.             i=++tot;
  78.             siz(i)=1;fa(i)=f;val(i)=k;
  79.             return;
  80.         }
  81.         if(x<=siz(ls(i))+1)  insert(ls(i),i,x,k);
  82.         else  insert(rs(i),i,x-siz(ls(i))-1,k);
  83.         up(i);
  84.     }
  85.     void out(int i){
  86.         down(i);
  87.         if(ls(i))  out(ls(i));
  88.         if(val(i)>1&&val(i)<=n+1)
  89.         write(val(i)-1),putchar(' ');
  90.         if(rs(i))  out(rs(i));
  91.     }
  92. } using namespace SPLAY;
  94. signed main()
  95. {
  96.     #ifndef ONLINE_JUDGE
  97.         freopen("lty.in","r",stdin);
  98.         freopen("lty.out","w",stdout);
  99.     #endif
  100.     n=read,m=read;
  101.     insert(rt,0,1,1);
  102.     for(int i=1;i<=n;i++){
  103.         insert(rt,0,i+1,i+1);
  104.         splay(tot,0);
  105.     }
  106.     insert(rt,0,n+2,n+2);
  107.     int l,r;
  108.     for(int i=1;i<=m;i++){
  109.         l=read+1,r=read+1;
  110.         splay(find(l-1),0);
  111.         splay(find(r+1),rt);
  112.         int p=ls(rs(rt));
  113.         lazy(p)^=1;
  114.     }
  115.     out(rt);
  116.     return 0;
  117. }

\(T_F\) 二逼平衡树

线段树套平衡树板子。

  • 首先建立普通线段树，对于每个区间建一棵平衡树。
  • 对于 \(x\) 区间内排名，转化成查找区间内比它小的树的个数加 \(1\)，分裂求。
  • 对于第 \(k\) 小数，考虑二分，通过操作 \(1\) 检查
  • 单点修改直接从根节点跑到叶子，路过的每个节点都要删掉原数，插入新数。注意要修改原序列。
  • 前驱后继直接分别查区间内每个小区间，取极值即可。

由于难写难调，只打了 FHQ_Treap

FHQ_Treap 
  1. #include<bits/stdc++.h>
  2. using namespace std;
  4. #define read read()
  5. #define pt puts("")
  6. inline int read{
  7.     int x=0,f=1;char c=getchar();
  8.     while(c<'0'||c>'9') {if(c=='-')  f=-1;c=getchar();}
  9.     while(c>='0'&&c<='9')   x=(x<<3)+(x<<1)+c-'0',c=getchar();
  10.     return f*x;
  11. }
  12. void write(int x){
  13.     if(x<0)  putchar('-'),x=-x;
  14.     if(x>9)  write(x/10);
  15.     putchar(x%10+'0');
  16.     return;
  17. }
  18. const int N = 5*1e4+10;
  19. const int inf = 2147483647;
  20. int n,a[N],m;
  21. int MIN=inf,MAX=-inf;
  23. namespace FHQ_TREAP{
  24.     struct Treap{
  25.         int son[2],rd,cnt,siz,val;
  26.         #define ls(i) t[i].son[0]
  27.         #define rs(i) t[i].son[1]
  28.         #define rd(i) t[i].rd
  29.         #define cnt(i) t[i].cnt
  30.         #define siz(i) t[i].siz
  31.         #define val(i) t[i].val
  32.     }t[N<<6];
  33.     int tot;
  34.     void up(int i){
  35.         siz(i)=siz(ls(i))+siz(rs(i))+cnt(i);
  36.     }
  37.     int New(int k){
  38.         val(++tot)=k;
  39.         siz(tot)=cnt(tot)=1;
  40.         rd(tot)=rand();
  41.         return tot;
  42.     }
  43.     void split(int i,int k,int &x,int &y){
  44.         if(!i){x=y=0;return;}
  45.         if(val(i)<=k)  x=i,split(rs(i),k,rs(i),y);
  46.         else  y=i,split(ls(i),k,x,ls(i));
  47.         up(i);
  48.     }
  49.     void merge(int &i,int x,int y){
  50.         if(!x||!y){i=x|y;return;}
  51.         if(rd(x)>rd(y))  merge(rs(x),rs(x),y),i=x;
  52.         else  merge(ls(y),x,ls(y)),i=y;
  53.         up(i);
  54.     }
  55.     void insert(int &rt,int k){
  56.         int rt1,rt2;
  57.         split(rt,k-1,rt1,rt2);
  58.         merge(rt,rt1,New(k));
  59.         merge(rt,rt,rt2);
  60.     }
  61.     void del(int &rt,int k){
  62.         int rt1,rt2,cut;
  63.         split(rt,k,rt1,rt2);
  64.         split(rt1,k-1,rt1,cut);
  65.         merge(cut,ls(cut),rs(cut));
  66.         merge(rt1,rt1,cut);
  67.         merge(rt,rt1,rt2);
  68.     }
  69.     int sumless(int rt,int k){
  70.         int rt1,rt2;
  71.         split(rt,k-1,rt1,rt2);
  72.         int res=siz(rt1);
  73.         merge(rt,rt1,rt2);
  74.         return res;
  75.     }
  76.     int pre(int rt,int k){
  77.         int rt1,rt2;
  78.         split(rt,k-1,rt1,rt2);
  79.         if(!siz(rt1))  return -inf;
  80.         int res=rt1;
  81.         while(rs(res))  res=rs(res);
  82.         merge(rt,rt1,rt2);
  83.         return val(res);
  84.     }
  85.     int nxt(int rt,int k){
  86.         int rt1,rt2;
  87.         split(rt,k,rt1,rt2);
  88.         if(!siz(rt2))  return inf;
  89.         int res=rt2;
  90.         while(ls(res))  res=ls(res);
  91.         merge(rt,rt1,rt2);
  92.         return val(res);
  93.     }
  94.     #undef ls
  95.     #undef rs
  96. };
  97. using namespace FHQ_TREAP;
  99. namespace Segment_Tree{
  100.     struct SegTree{
  101.         int l,r,rt;
  102.         #define l(i) tr[i].l
  103.         #define r(i) tr[i].r
  104.         #define rt(i) tr[i].rt
  105.         #define ls(i) (i<<1)
  106.         #define rs(i) (i<<1|1)
  107.     }tr[N<<2];
  108.     void build(int i,int l,int r){
  109.         l(i)=l,r(i)=r;
  110.         for(int k=l;k<=r;k++){
  111.             insert(rt(i),a[k]);
  112.         }
  113.         if(l==r)  return;
  114.         int mid=(l+r)>>1;
  115.         build(ls(i),l,mid);
  116.         build(rs(i),mid+1,r);
  117.     }
  118.     int lessk(int i,int ql,int qr,int k){
  119.         int l=l(i),r=r(i);
  120.         if(ql<=l&&r<=qr){
  121.             return sumless(rt(i),k);
  122.         }
  123.         int mid=(l+r)>>1,res=0;
  124.         if(ql<=mid)  res+=lessk(ls(i),ql,qr,k);
  125.         if(mid<qr)  res+=lessk(rs(i),ql,qr,k);
  126.         return res;
  127.     }
  128.     int q_rk(int ql,int qr,int k){
  129.         return lessk(1,ql,qr,k)+1;
  130.     }
  131.     int q_kth(int ql,int qr,int k){
  132.         int st=MIN,ed=MAX,res=0;
  133.         while(st<=ed){
  134.             int mid=(st+ed)>>1;
  135.             if(q_rk(ql,qr,mid)<=k)
  136.                 res=mid,st=mid+1;
  137.             else  ed=mid-1;
  138.         }
  139.         return res;
  140.     }
  141.     void modify(int i,int x,int k){
  142.         del(rt(i),a[x]);
  143.         insert(rt(i),k);
  144.         int l=l(i),r=r(i);
  145.         if(l==r)  return;
  146.         int mid=(l+r)>>1;
  147.         if(x<=mid)  modify(ls(i),x,k);
  148.         else  modify(rs(i),x,k);
  149.     }
  150.     int q_pre(int i,int ql,int qr,int k){
  151.         int l=l(i),r=r(i);
  152.         if(ql<=l&&r<=qr){
  153.             return pre(rt(i),k);
  154.         }
  155.         int mid=(l+r)>>1,res=-inf;
  156.         if(ql<=mid) res=max(res,q_pre(ls(i),ql,qr,k));
  157.         if(mid<qr)  res=max(res,q_pre(rs(i),ql,qr,k));
  158.         return res;
  159.     }
  160.     int q_nxt(int i,int ql,int qr,int k){
  161.         int l=l(i),r=r(i);
  162.         if(ql<=l&&r<=qr){
  163.             return nxt(rt(i),k);
  164.         }
  165.         int mid=(l+r)>>1,res=inf;
  166.         if(ql<=mid)  res=min(res,q_nxt(ls(i),ql,qr,k));
  167.         if(mid<qr)   res=min(res,q_nxt(rs(i),ql,qr,k));
  168.         return res;
  169.     }
  170. };
  171. using namespace Segment_Tree;
  173. signed main()
  174. {
  175.     srand(time(0));
  176.     #ifndef ONLINE_JUDGE
  177.         freopen("lty.in","r",stdin);
  178.         freopen("lty.out","w",stdout);
  179.     #endif
  180.     n=read,m=read;
  181.     for(int i=1;i<=n;i++)  a[i]=read,MIN=min(MIN,a[i]),MAX=max(MAX,a[i]);
  182.     build(1,1,n);
  183.     int op,l,r,x;
  184.     while(m-->0){
  185.         op=read;
  186.         switch(op){
  187.             case 1:
  188.                 l=read,r=read,x=read;
  189.                 write(q_rk(l,r,x)),pt;break;
  190.             case 2:
  191.                 l=read,r=read,x=read;
  192.                 write(q_kth(l,r,x)),pt;break;
  193.             case 3:
  194.                 l=read,x=read;//不要忘记修改原序列
  195.                 modify(1,l,x);a[l]=x;break;
  196.             case 4:
  197.                 l=read,r=read,x=read;
  198.                 write(q_pre(1,l,r,x)),pt;break;
  199.             case 5:
  200.                 l=read,r=read,x=read;
  201.                 write(q_nxt(1,l,r,x)),pt;break;
  202.             default:break;
  203.         }
  204.     }
  205.     return 0;
  206. }

服了，洛谷数据太强大，我的常数也太强大，不得不写离散化。。

FHQ_Treap+离散化 
  1. #include<bits/stdc++.h>
  2. #define getchar() getchar_unlocked()
  3. using namespace std;
  5. #define read read()
  6. #define pt puts("")
  7. inline int read{
  8.     int x=0,f=1;char c=getchar();
  9.     while(c<'0'||c>'9') {if(c=='-')  f=-1;c=getchar();}
  10.     while(c>='0'&&c<='9')   x=(x<<3)+(x<<1)+c-'0',c=getchar();
  11.     return f*x;
  12. }
  13. void write(int x){
  14.     if(x<0)  putchar('-'),x=-x;
  15.     if(x>9)  write(x/10);
  16.     putchar(x%10+'0');
  17.     return;
  18. }
  19. const int N = 5*1e4+10;
  20. const int inf = 2147483647;
  21. int n,a[N],m;
  22. int MIN=inf,MAX=-inf;
  23. int lsh[N<<1],num,tt;
  24. int op[N];
  25. int l[N],r[N],x[N];
  26. int ans[N],total;
  28. namespace FHQ_TREAP{
  29.     struct Treap{
  30.         int son[2],rd,cnt,siz,val;
  31.         #define ls(i) t[i].son[0]
  32.         #define rs(i) t[i].son[1]
  33.         #define rd(i) t[i].rd
  34.         #define cnt(i) t[i].cnt
  35.         #define siz(i) t[i].siz
  36.         #define val(i) t[i].val
  37.     }t[N<<6];
  38.     int tot;
  39.     void up(int i){
  40.         siz(i)=siz(ls(i))+siz(rs(i))+cnt(i);
  41.     }
  42.     int New(int k){
  43.         val(++tot)=k;
  44.         siz(tot)=cnt(tot)=1;
  45.         rd(tot)=rand();
  46.         return tot;
  47.     }
  48.     void split(int i,int k,int &x,int &y){
  49.         if(!i){x=y=0;return;}
  50.         if(val(i)<=k)  x=i,split(rs(i),k,rs(i),y);
  51.         else  y=i,split(ls(i),k,x,ls(i));
  52.         up(i);
  53.     }
  54.     void merge(int &i,int x,int y){
  55.         if(!x||!y){i=x|y;return;}
  56.         if(rd(x)>rd(y))  merge(rs(x),rs(x),y),i=x;
  57.         else  merge(ls(y),x,ls(y)),i=y;
  58.         up(i);
  59.     }
  60.     void insert(int &rt,int k){
  61.         int rt1,rt2;
  62.         split(rt,k-1,rt1,rt2);
  63.         merge(rt,rt1,New(k));
  64.         merge(rt,rt,rt2);
  65.     }
  66.     void del(int &rt,int k){
  67.         int rt1,rt2,cut;
  68.         split(rt,k,rt1,rt2);
  69.         split(rt1,k-1,rt1,cut);
  70.         merge(cut,ls(cut),rs(cut));
  71.         merge(rt1,rt1,cut);
  72.         merge(rt,rt1,rt2);
  73.     }
  74.     int sumless(int rt,int k){
  75.         int rt1,rt2;
  76.         split(rt,k-1,rt1,rt2);
  77.         int res=siz(rt1);
  78.         merge(rt,rt1,rt2);
  79.         return res;
  80.     }
  81.     int pre(int rt,int k){
  82.         int rt1,rt2;
  83.         split(rt,k-1,rt1,rt2);
  84.         if(!siz(rt1))  return -inf;
  85.         int res=rt1;
  86.         while(rs(res))  res=rs(res);
  87.         merge(rt,rt1,rt2);
  88.         return val(res);
  89.     }
  90.     int nxt(int rt,int k){
  91.         int rt1,rt2;
  92.         split(rt,k,rt1,rt2);
  93.         if(!siz(rt2))  return inf;
  94.         int res=rt2;
  95.         while(ls(res))  res=ls(res);
  96.         merge(rt,rt1,rt2);
  97.         return val(res);
  98.     }
  99.     #undef ls
  100.     #undef rs
  101. };
  102. using namespace FHQ_TREAP;
  104. namespace Segment_Tree{
  105.     struct SegTree{
  106.         int l,r,rt;
  107.         #define l(i) tr[i].l
  108.         #define r(i) tr[i].r
  109.         #define rt(i) tr[i].rt
  110.         #define ls(i) (i<<1)
  111.         #define rs(i) (i<<1|1)
  112.     }tr[N<<2];
  113.     void build(int i,int l,int r){
  114.         l(i)=l,r(i)=r;
  115.         for(int k=l;k<=r;k++){
  116.             insert(rt(i),a[k]);
  117.         }
  118.         if(l==r)  return;
  119.         int mid=(l+r)>>1;
  120.         build(ls(i),l,mid);
  121.         build(rs(i),mid+1,r);
  122.     }
  123.     int lessk(int i,int ql,int qr,int k){
  124.         int l=l(i),r=r(i);
  125.         if(ql<=l&&r<=qr){
  126.             return sumless(rt(i),k);
  127.         }
  128.         int mid=(l+r)>>1,res=0;
  129.         if(ql<=mid)  res+=lessk(ls(i),ql,qr,k);
  130.         if(mid<qr)  res+=lessk(rs(i),ql,qr,k);
  131.         return res;
  132.     }
  133.     int q_rk(int ql,int qr,int k){
  134.         return lessk(1,ql,qr,k)+1;
  135.     }
  136.     int q_kth(int ql,int qr,int k){
  137.         int st=0,ed=num,res=0;
  138.         while(st<=ed){
  139.             int mid=(st+ed)>>1;
  140.             if(q_rk(ql,qr,mid)<=k)
  141.                 res=mid,st=mid+1;
  142.             else  ed=mid-1;
  143.         }
  144.         return res;
  145.     }
  146.     void modify(int i,int x,int k){
  147.         del(rt(i),a[x]);
  148.         insert(rt(i),k);
  149.         int l=l(i),r=r(i);
  150.         if(l==r)  return;
  151.         int mid=(l+r)>>1;
  152.         if(x<=mid)  modify(ls(i),x,k);
  153.         else  modify(rs(i),x,k);
  154.     }
  155.     int q_pre(int i,int ql,int qr,int k){
  156.         int l=l(i),r=r(i);
  157.         if(ql<=l&&r<=qr){
  158.             return pre(rt(i),k);
  159.         }
  160.         int mid=(l+r)>>1,res=-inf;
  161.         if(ql<=mid) res=max(res,q_pre(ls(i),ql,qr,k));
  162.         if(mid<qr)  res=max(res,q_pre(rs(i),ql,qr,k));
  163.         return res;
  164.     }
  165.     int q_nxt(int i,int ql,int qr,int k){
  166.         int l=l(i),r=r(i);
  167.         if(ql<=l&&r<=qr){
  168.             return nxt(rt(i),k);
  169.         }
  170.         int mid=(l+r)>>1,res=inf;
  171.         if(ql<=mid)  res=min(res,q_nxt(ls(i),ql,qr,k));
  172.         if(mid<qr)   res=min(res,q_nxt(rs(i),ql,qr,k));
  173.         return res;
  174.     }
  175. };
  176. using namespace Segment_Tree;
  178. void LSH(){
  179.     sort(lsh+1,lsh+tt+1);
  180.     num=unique(lsh+1,lsh+tt+1)-lsh-1;
  181.     for(int i=1;i<=n;i++){
  182.         a[i]=lower_bound(lsh+1,lsh+num+1,a[i])-lsh;
  183.     }
  184. }
  186. signed main()
  187. {
  188.     srand(time(0));
  189.     #ifndef ONLINE_JUDGE
  190.         freopen("lty.in","r",stdin);
  191.         freopen("lty.out","w",stdout);
  192.     #endif
  193.     n=read,m=read;
  194.     for(int i=1;i<=n;i++)  a[i]=lsh[++tt]=read;
  195.     for(int i=1;i<=m;i++){
  196.         op[i]=read;
  197.         switch(op[i]){
  198.             case 1:
  199.                 l[i]=read,r[i]=read,x[i]=read;break;
  200.             case 2:
  201.                 l[i]=read,r[i]=read,x[i]=read;break;
  202.             case 3:
  203.                 l[i]=read,x[i]=read;
  204.                 lsh[++tt]=x[i];break;
  205.             case 4:
  206.                 l[i]=read,r[i]=read,x[i]=read;
  207.                 lsh[++tt]=x[i];break;
  208.             case 5:
  209.                 l[i]=read,r[i]=read,x[i]=read;
  210.                 lsh[++tt]=x[i];break;
  211.             default:break;
  212.         }
  213.     }
  214.     LSH();
  215.     build(1,1,n);
  216.     for(int i=1;i<=m;i++){
  217.         int an;
  218.         switch(op[i]){
  219.             case 1:
  220.                 x[i]=lower_bound(lsh+1,lsh+num+1,x[i])-lsh;
  221.                 ans[++total]=q_rk(l[i],r[i],x[i]);break;
  222.             case 2:
  223.                 ans[++total]=lsh[q_kth(l[i],r[i],x[i])];break;
  224.             case 3:
  225.                 x[i]=lower_bound(lsh+1,lsh+num+1,x[i])-lsh;
  226.                 modify(1,l[i],x[i]);a[l[i]]=x[i];break;
  227.             case 4:
  228.                 x[i]=lower_bound(lsh+1,lsh+num+1,x[i])-lsh;
  229.                 an=q_pre(1,l[i],r[i],x[i]);
  230.                 ans[++total]=(an==-inf?-inf:lsh[an]);break;
  231.             case 5:
  232.                 x[i]=lower_bound(lsh+1,lsh+num+1,x[i])-lsh;
  233.                 an=q_nxt(1,l[i],r[i],x[i]);
  234.                 ans[++total]=(an==inf?inf:lsh[an]);break;
  235.             default:break;
  236.         }
  237.     }
  238.     for(int i=1;i<=total;i++)  write(ans[i]),pt;
  239.     return 0;
  240. }

\(T_G\) JSOI2008火星人prefix

平衡树维护序列，\(\tt{FHQ}\) 按子树大小分裂，维护 \(hash\) 值，父节点存子树的 \(hash\) 值，最后二分求 \(LCP\)。注意插入字符后要 ++n。

还是 \(\tt{FHQ}\) 好打，\(\tt{Splay}\) 以后再说。

FHQ_Treap 
  1. #include<bits/stdc++.h>
  2. using namespace std;
  3. #define  ull unsigned long long
  4. #define read read()
  5. #define pt puts("")
  6. #define gc getchar
  7. inline int read{
  8.     int x=0,f=1;char c=getchar();
  9.     while(c<'0'||c>'9') {if(c=='-')  f=-1;c=getchar();}
  10.     while(c>='0'&&c<='9')   x=(x<<3)+(x<<1)+c-'0',c=getchar();
  11.     return f*x;
  12. }
  13. void write(int x){
  14.     if(x<0)  putchar('-'),x=-x;
  15.     if(x>9)  write(x/10);
  16.     putchar(x%10+'0');
  17.     return;
  18. }
  19. #define N 100010
  20. const ull base = 233;
  22. int n,m;
  23. char s[N];
  25. ull pb[N];
  26. void init(){pb[0]=1ull;for(int i=1;i<N;i++)pb[i]=pb[i-1]*base;}
  28. namespace FHQ_Treap{
  29.     struct Treap{
  30.         int son[2],rd,siz,val;
  31.         ull hash;
  32.         #define ls(i) t[i].son[0]
  33.         #define rs(i) t[i].son[1]
  34.         #define rd(i) t[i].rd
  35.         #define siz(i) t[i].siz
  36.         #define val(i) t[i].val
  37.         #define hash(i) t[i].hash
  38.     }t[N<<1];
  39.     int tot,rt;
  40.     void up(int i){
  41.         siz(i)=1+siz(ls(i))+siz(rs(i));
  42.         hash(i)=hash(ls(i))*(pb[siz(rs(i))+1])+val(i)*pb[siz(rs(i))]+hash(rs(i));
  43.     }
  44.     int New(int k){
  45.         val(++tot)=k;
  46.         hash(tot)=k;
  47.         siz(tot)=1;
  48.         rd(tot)=rand();
  49.         return tot;
  50.     }
  51.     void split(int i,int k,int &x,int &y){
  52.         if(!i){x=y=0;return;}
  53.         if(k<=siz(ls(i)))  y=i,split(ls(i),k,x,ls(i));
  54.         else  x=i,split(rs(i),k-(siz(ls(i))+1),rs(i),y);
  55.         up(i);
  56.     }
  57.     void merge(int &i,int x,int y){
  58.         if(!x||!y){i=x|y;return;}
  59.         if(rd(x)>rd(y))  merge(rs(x),rs(x),y),i=x;
  60.         else  merge(ls(y),x,ls(y)),i=y;
  61.         up(i);
  62.     }
  63.     void insert(int x,int k){
  64.         int rt1,rt2;
  65.         split(rt,x,rt1,rt2);
  66.         merge(rt,rt1,New(k));
  67.         merge(rt,rt,rt2);
  68.     }
  69.     void replace(int x,int k){
  70.         int rt1,rt2,rt3;
  71.         split(rt,x,rt1,rt2);
  72.         split(rt1,x-1,rt1,rt3);
  73.         merge(rt1,rt1,New(k));
  74.         merge(rt,rt1,rt2);
  75.     }
  76.     ull q_hash(int l,int r){
  77.         int rt1,rt2,rt3;
  78.         split(rt,r,rt2,rt3);
  79.         split(rt2,l-1,rt1,rt2);
  80.         ull res=hash(rt2);
  81.         merge(rt2,rt1,rt2);
  82.         merge(rt,rt2,rt3);
  83.         return res;
  84.     }
  85. } using namespace FHQ_Treap;
  87. int solve(int l,int r){
  88.     int st=0,ed=n-r+1;
  89.     int res=0;
  90.     while(st<=ed){
  91.         int mid=(st+ed)>>1;
  92.         if(q_hash(l,l+mid-1)==q_hash(r,r+mid-1)){
  93.             st=mid+1;res=mid;
  94.         }
  95.         else  ed=mid-1;
  96.     }
  97.     return res;
  98. }
  100. signed main()
  101. {
  102.     #ifndef ONLINE_JUDGE
  103.         freopen("lty.in","r",stdin);
  104.         freopen("lty.out","w",stdout);
  105.     #endif
  106.     scanf("%s",s+1);
  107.     n=strlen(s+1);m=read;
  108.     init();
  109.     for(int i=1;i<=n;i++){
  110.         insert(i-1,s[i]-'a'+1);
  111.     }
  112.     char op,x;
  113.     int l,r;
  114.     while(m-->0){
  115.         op=gc();while(op!='Q'&&op!='R'&&op!='I')op=gc();
  116.         switch(op){
  117.             case 'Q':
  118.                 l=read,r=read;
  119.                 write(solve(l,r)),pt;
  120.                 break;
  121.             case 'R':
  122.                 l=read;x=gc();while(x<'a'||x>'z')  x=gc();
  123.                 replace(l,x-'a'+1);
  124.                 break;
  125.             case 'I':
  126.                 l=read;x=gc();while(x<'a'||x>'z')  x=gc();
  127.                 insert(l,x-'a'+1);++n;
  128.                 break;
  129.             default:break;
  130.         }
  131.     }
  133.     return 0;
  134. }

\(T_H\) 最长上升子序列

逆天性质题~~

本来对于 \(dp_i\) 表示以 \(i\) 位置结尾的最长上升子序列长度，有:

\[dp_i = \max_{1\leq j\leq i}^{a_j<a_i}dp_j + 1 \]

但是对于此题，他是按照 \(1\) ~ \(n\) 的顺序插入，也就是，当前插入的数，一定比原序列里所有数都大，那么

\[dp_i = \max_{1\leq j\leq i}dp_j + 1 \]

考虑平衡树维护序列，节点存子树里的 \(dp\) 最大值，直接转移即可。

  • 对于 \(\tt{FHQ}\)，分裂出前 \(i\) 个，\(rt1\) 的 \(dp\) 值 \(\tt{+1}\) 即为所求
  • 对于 \(\tt{Splay}\)，转到根节点，左儿子的 \(dp\) 值 \(\tt{+1}\) 即为所求
FHQ_Treap 
  1. #include<bits/stdc++.h>
  2. using namespace std;
  4. #define read read()
  5. #define pt puts("")
  6. inline int read{
  7.     int x=0,f=1;char c=getchar();
  8.     while(c<'0'||c>'9') {if(c=='-')  f=-1;c=getchar();}
  9.     while(c>='0'&&c<='9')   x=(x<<3)+(x<<1)+c-'0',c=getchar();
  10.     return f*x;
  11. }
  12. void write(int x){
  13.     if(x<0)  putchar('-'),x=-x;
  14.     if(x>9)  write(x/10);
  15.     putchar(x%10+'0');
  16.     return;
  17. }
  18. const int N = 1e5+10;
  19. int n;
  21. namespace FHQ_Treap{
  22.     struct Treap{
  23.         int son[2],rd,siz,len,ans;
  24.         #define ls(i) t[i].son[0]
  25.         #define rs(i) t[i].son[1]
  26.         #define rd(i) t[i].rd
  27.         #define siz(i) t[i].siz
  28.         #define len(i) t[i].len
  29.         #define ans(i) t[i].ans
  30.     }t[N];
  31.     int tot,rt;
  32.     void up(int i){
  33.         siz(i)=siz(ls(i))+siz(rs(i))+1;
  34.         ans(i)=max(ans(ls(i)),ans(rs(i)));
  35.         ans(i)=max(ans(i),len(i));
  36.     }
  37.     void split(int i,int k,int &x,int &y){
  38.         if(!i){x=y=0;return;}
  39.         if(k<=siz(ls(i)))  y=i,split(ls(i),k,x,ls(i));
  40.         else  x=i,split(rs(i),k-(siz(ls(i))+1),rs(i),y);
  41.         up(i);
  42.     }
  43.     void merge(int &i,int x,int y){
  44.         if(!x||!y){i=x|y;return;}
  45.         if(rd(x)>rd(y))  merge(rs(x),rs(x),y),i=x;
  46.         else  merge(ls(y),x,ls(y)),i=y;
  47.         up(i);
  48.     }
  49.     int New(int k){
  50.         ++tot;
  51.         siz(tot)=1;
  52.         ans(tot)=len(tot)=k;
  53.         rd(tot)=rand();
  54.         return tot;
  55.     }
  56.     void insert(int x){
  57.         int rt1,rt2;
  58.         split(rt,x,rt1,rt2);
  59.         merge(rt,rt1,New(ans(rt1)+1));
  60.         merge(rt,rt,rt2);
  61.     }
  63. } using namespace FHQ_Treap;
  65. signed main()
  66. {
  67.     #ifndef ONLINE_JUDGE
  68.         freopen("lty.in","r",stdin);
  69.         freopen("lty.out","w",stdout);
  70.     #endif
  71.     n=read;
  72.     for(int x,i=1;i<=n;i++){
  73.         x=read;
  74.         insert(x);
  75.         write(ans(rt));pt;
  76.     }
  77.     return 0;
  78. }
Splay 
  1. #include<bits/stdc++.h>
  2. using namespace std;
  4. #define read read()
  5. #define pt puts("")
  6. inline int read{
  7.     int x=0,f=1;char c=getchar();
  8.     while(c<'0'||c>'9') {if(c=='-')  f=-1;c=getchar();}
  9.     while(c>='0'&&c<='9')   x=(x<<3)+(x<<1)+c-'0',c=getchar();
  10.     return f*x;
  11. }
  12. void write(int x){
  13.     if(x<0)  putchar('-'),x=-x;
  14.     if(x>9)  write(x/10);
  15.     putchar(x%10+'0');
  16.     return;
  17. }
  18. const int N = 1e5+10;
  19. int n;
  21. namespace SPLAY{
  22.     struct Splay_Tree{
  23.         int son[2],fa,ans,siz,val;
  24.         #define ls(i) t[i].son[0]
  25.         #define rs(i) t[i].son[1]
  26.         #define ds(i) t[i].son[d]
  27.         #define bs(i) t[i].son[d^1]
  28.         #define fa(i) t[i].fa
  29.         #define siz(i) t[i].siz
  30.         #define ans(i) t[i].ans
  31.         #define val(i) t[i].val
  32.     }t[N];
  33.     int tot,rt;
  34.     void up(int i){
  35.         siz(i)=siz(ls(i))+siz(rs(i))+1;
  36.         ans(i)=max(ans(ls(i)),ans(rs(i)));
  37.         ans(i)=max(ans(i),val(i));
  38.     }
  39.     void rotate(int x){
  40.         int y=fa(x),z=fa(y);
  41.         int d=(rs(y)==x);
  42.         t[z].son[(rs(z)==y)]=x;fa(x)=z;
  43.         ds(y)=bs(x);fa(bs(x))=y;
  44.         bs(x)=y;fa(y)=x;
  45.         up(y),up(x);
  46.     }
  47.     void splay(int x,int s){
  48.         while(fa(x)!=s){
  49.             int y=fa(x),z=fa(y);
  50.             if(z!=s)
  51.                 (ls(y)==x)^(ls(z)==y)?rotate(x):rotate(y);
  52.             rotate(x);
  53.         }
  54.         if(!s)  rt=x;
  55.     }
  56.     void find(int x){
  57.         if(!rt)  return;
  58.         int p=rt;
  59.         while(siz(ls(p))+1!=x){
  60.             if(x<=siz(ls(p))+1){
  61.                 p=ls(p);
  62.             }
  63.             else{
  64.                 x-=(siz(ls(p))+1);
  65.                 p=rs(p);
  66.             }
  67.         }
  68.         splay(p,0);
  69.     }
  70.     void insert(int &i,int f,int x,int k){
  71.         if(!i){
  72.             i=++tot;
  73.             fa(i)=f;
  74.             siz(i)=1;
  75.             ans(i)=val(i)=k;
  76.             return;
  77.         }
  78.         if(x<=siz(ls(i))+1)  insert(ls(i),i,x,k);
  79.         else  insert(rs(i),i,x-siz(ls(i))-1,k);
  80.         up(i);
  81.     }
  82.     
  83. } using namespace SPLAY;
  86. signed main()
  87. {
  88.     #ifndef ONLINE_JUDGE
  89.         freopen("lty.in","r",stdin);
  90.         freopen("lty.out","w",stdout);
  91.     #endif
  92.     n=read;
  93.     for(int x,k,i=1;i<=n;i++){
  94.         x=read;
  95.         if(!x)  k=1;
  96.         else if(x==i-1)  k=ans(rt)+1;
  97.         else{
  98.             find(x+1);
  99.             k=ans(ls(rt))+1;
  100.         }
  101.         insert(rt,0,x+1,k);
  102.         splay(tot,0);
  103.         write(ans(rt));pt;
  104.     }
  105.     return 0;
  106. }

\(T_I\) 星系探索

好像是阉割版的 \(\tt{ETT/LCT}\)(Wang54321说的)，不会。

伍.闲话

转眼间在奥赛班的短短 \(3\) 个月只剩最后几天，整个下午跑机房，还能有多长时间。。。\(3\) 个月说长不长说短不短，学到了不少东西，虽然不像别的奥赛对高中文化课有很大帮助，但是:

我们学的东西是他们这辈子都不一定能接触到的。。。

不知道回原班在中考前还能学多长时间 \(\tt{OI}\)，像小 \(\tt{H}\) 说的

也不知道回原班之后的二三十天，自己还能在这个机位上坐几个小时。这种感觉，或有点像心有余而力不足而被迫退役的感觉吧。当然我也希望，两年后的自己，不会有这种感觉。——\(\tt{HANGRY\_ Sol}\)

没想到二模完没有立刻【垃圾分类】，那就把 \(\tt{Splay}\) 收尾，不用放假加班了，珍惜机房的每一分钟吧...

原文链接：https://www.cnblogs.com/lty-ylzsx/p/18211987

 友情链接：直通硅谷 　点职佳 　北美留学生论坛

编程经验热门文章

  • Prometheus监控之SNMP Exporter介绍和数据展现
  • Intel 82599网卡异常挂死原因
  • 腾讯防水墙的分析识别与破解
  • 桌面应用自动化WinAppDriver入门
  • 文档在线预览（三）使用js前端实现word、excel、pdf、ppt 在线预览
  • 「教程」如何下载AcFun网站上的视频、A站视频下载工具
  • 基于Hi3559AV100的SVP(NNIE)开发整体流程
  • GBDT(梯度提升树)scikit-klearn中的参数说明及简汇
  • antd之RangePicker设置默认值方式
  • 决胜经典算法之插入排序

    • 编程经验推荐文章

  • wifi基础(一)：无线电波与WIFI信号干扰、衰减
  • 甲方扔给两个存在包名与类名均相同的Jar包，要在工程中同时使用怎么办？
  • 《花100块做个摸鱼小网站! 》第三篇—热搜表结构设计和热搜数据存储
  • Fluent Editor：一个基于 Quill 2.0 的富文本编辑器，功能强大、开箱即用！
  • 方法的三种调用形式
  • 《花100块做个摸鱼小网站! 》第二篇—后端应用搭建和完成第一个爬虫
  • 《熬夜整理》保姆级系列教程-玩转Wireshark抓包神器教程(4)-再识Wireshark - 北京-宏哥
  • 《软件性能测试分析与调优实践之路》(第2版) 读书笔记（二）总体介绍（下）-真正从性能分析与调优来看性能测试
  • 架构知识点（三）
  • 《花100块做个摸鱼小网站! 》第一篇—买云服务器和初始化环境

    • 本站QQ群：前端 618073944 | Java 606181507 | Python 626812652 | C/C++ 612253063 | 微信 634508462 | 苹果 692586424 | C#/.net 182808419 | PHP 305140648 | 运维 608723728

    W3xue 的所有内容仅供测试，对任何法律问题及风险不承担任何责任。通过使用本站内容随之而来的风险与本站无关。
    关于我们  |  意见建议  |  捐助我们  |  报错有奖  |  广告合作、友情链接（目前9元/月）请联系QQ：27243702 沸活量
    皖ICP备17017327号-2　皖公网安备34020702000426号