话接上回《前端使用 Konva 实现可视化设计器(13)- 折线 - 最优路径应用【思路篇】》,这一章继续说说相关的代码如何构思的,如何一步步构建数据模型可供 AStar 算法进行路径规划,最终画出节点之间的连接折线。
请大家动动小手,给我一个免费的 Star 吧~
大家如果发现了 Bug,欢迎来提 Issue 哟~
github源码
gitee源码
示例地址
补充说明
上一章说到使用了开源 AStar 算法,它并不支持计算折线拐弯的代价,最终结果会出现不必要的拐弯,现已经把算法替换成自定义 AStar 算法,支持计算拐弯代价,减少了不必要的折线拐弯。
AStar 算法基本逻辑可以参考《C++: A*(AStar)算法》,本示例的自定义 AStar 算法,是在此基础上增加支持:格子代价、拐弯代价。
代码不长,可以直接看看:
关键要理解 AStar 算法的基本思路,特别是“open 和 closed 列表”、“每个节点的 f, g, h 值”
// src\Render\utils\aStar.tsexport interface Node { x: number y: number cost?: number parent?: Node}export default function aStar(config: { from: Node to: Node matrix: number[][] maxCost: number}): Node[] { const { from, to, matrix, maxCost = 1 } = config const grid: Node[][] = matrixToGrid(matrix) const start = grid[from.y][from.x] const goal = grid[to.y][to.x] // 初始化 open 和 closed 列表 const open: Node[] = [start] const closed = new Set<Node>() // 初始化每个节点的 f, g, h 值 const f = new Map<Node, number>() const g = new Map<Node, number>() const h = new Map<Node, number>() g.set(start, 0) h.set(start, manhattanDistance(start, goal)) f.set(start, g.get(start)! + h.get(start)!) // A* 算法主循环 while (open.length > 0) { // 从 open 列表中找到 f 值最小的节点 const current = open.reduce((a, b) => (f.get(a)! < f.get(b)! ? a : b)) // 如果当前节点是目标节点,返回路径 if (current === goal) { return reconstructPath(goal) } // 将当前节点从 open 列表中移除,并加入 closed 列表 open.splice(open.indexOf(current), 1) closed.add(current) // 遍历当前节点的邻居 for (const neighbor of getNeighbors(current, grid)) { // 如果邻居节点已经在 closed 列表中,跳过 if (closed.has(neighbor)) { continue } // 计算从起点到邻居节点的距离(转弯距离增加) const tentativeG = g.get(current)! + (neighbor.cost ?? 0) + ((current.x === current.parent?.x && current.x !== neighbor.x) || (current.y === current.parent?.y && current.y !== neighbor.y) ? Math.max(grid.length, grid[0].length) : 0) // 如果邻居节点不在 open 列表中,或者新的 g 值更小,更新邻居节点的 g, h, f 值,并将其加入 open 列表 if (!open.includes(neighbor) || tentativeG < g.get(neighbor)!) { g.set(neighbor, tentativeG) h.set(neighbor, manhattanDistance(neighbor, goal)) f.set(neighbor, g.get(neighbor)! + h.get(neighbor)!) neighbor.parent = current if (!open.includes(neighbor)) { open.push(neighbor) } } } } // 如果 open 列表为空,表示无法到达目标节点,返回 null return [] // 数据转换 function matrixToGrid(matrix: number[][]) { const mt: Node[][] = [] for (let y = 0; y < matrix.length; y++) { if (mt[y] === void 0) { mt[y] = [] } for (let x = 0; x < matrix[y].length; x++) { mt[y].push({ x, y, cost: matrix[y][x] }) } } return mt } // 从目标节点开始,沿着 parent 指针重构路径 function reconstructPath(node: Node): Node[] { const path = [node] while (node.parent) { path.push(node.parent) node = node.parent } return path.reverse() } // 计算曼哈顿距离 function manhattanDistance(a: Node, b: Node): number { return Math.abs(a.x - b.x) + Math.abs(a.y - b.y) } // 获取当前节点的邻居 function getNeighbors(node: Node, grid: Node[][]): Node[] { const neighbors = [] const { x, y } = node if (x > 0 && (grid[y][x - 1].cost ?? 0) < maxCost) { neighbors.push(grid[y][x - 1]) } if (x < grid[0].length - 1 && (grid[y][x + 1].cost ?? 0) < maxCost) { neighbors.push(grid[y][x + 1]) } if (y > 0 && (grid[y - 1][x].cost ?? 0) < maxCost) { neighbors.push(grid[y - 1][x]) } if (y < grid.length - 1 && (grid[y + 1][x].cost ?? 0) < maxCost) { neighbors.push(grid[y + 1][x]) } return neighbors }}
在数据结构上,还有优化空间,应该可以减少性能和内存的消耗,暂且如此。
算法建模
主要逻辑在 src\Render\draws\LinkDraw.ts 的 draw 方法的画连接线的部分:
事前准备,把所有 节点、连接点、连接对 整理出来:
override draw() { this.clear() // stage 状态 const stageState = this.render.getStageState() const groups = this.render.layer.find('.asset') as Konva.Group[] const points = groups.reduce((ps, group) => { return ps.concat(Array.isArray(group.getAttr('points')) ? group.getAttr('points') : []) }, [] as LinkDrawPoint[]) const pairs = points.reduce((ps, point) => { return ps.concat(point.pairs ? point.pairs : []) }, [] as LinkDrawPair[]) // 略 }
主要逻辑,请看代码备注(一些工具方法,后面单独说明):
override draw() { // 略 // 连接线(根据连接对绘制) for (const pair of pairs) { // 连接起点节点、连接点 const fromGroup = groups.find((o) => o.id() === pair.from.groupId) const fromPoint = points.find((o) => o.id === pair.from.pointId) // 连接终点节点、连接点 const toGroup = groups.find((o) => o.id() === pair.to.groupId) const toPoint = points.find((o) => o.id === pair.to.pointId) // 最小区域 const fromGroupLinkArea = this.getGroupLinkArea(fromGroup) const toGroupLinkArea = this.getGroupLinkArea(toGroup) // 两区域的最短距离(用于动态缩短连接点及其出入口的距离) const groupDistance = this.getGroupPairDistance(fromGroupLinkArea, toGroupLinkArea) // 不可通过区域 const fromGroupForbiddenArea = this.getGroupForbiddenArea( fromGroupLinkArea, groupDistance - 2 ) const toGroupForbiddenArea = this.getGroupForbiddenArea(toGroupLinkArea, groupDistance - 2) // 两区域扩展 const groupForbiddenArea = this.getGroupPairArea(fromGroupForbiddenArea, toGroupForbiddenArea) // 连线通过区域 const groupAccessArea = this.getGroupPairArea( this.getGroupAccessArea(fromGroupForbiddenArea, groupDistance), this.getGroupAccessArea(toGroupForbiddenArea, groupDistance) ) if (fromGroup && toGroup && fromPoint && toPoint) { // 起点、终点的锚点 const fromAnchor = fromGroup.findOne(`#${fromPoint.id}`) const toAnchor = toGroup.findOne(`#${toPoint.id}`) // 锚点信息 const fromAnchorPos = this.getAnchorPos(fromAnchor) const toAnchorPos = this.getAnchorPos(toAnchor) if (fromAnchor && toAnchor) { // 连接出入口 const fromEntry: Konva.Vector2d = this.getEntry( fromAnchor, fromGroupLinkArea, groupDistance ) const toEntry: Konva.Vector2d = this.getEntry(toAnchor, toGroupLinkArea, groupDistance) type matrixPoint = { x: number y: number type?: 'from' | 'to' | 'from-entry' | 'to-entry' } // 可能点(人为定义的希望折线可以拐弯的位置) let matrixPoints: matrixPoint[] = [] // 通过区域 四角 matrixPoints.push({ x: groupAccessArea.x1, y: groupAccessArea.y1 }) matrixPoints.push({ x: groupAccessArea.x2, y: groupAccessArea.y2 }) matrixPoints.push({ x: groupAccessArea.x1, y: groupAccessArea.y2 }) matrixPoints.push({ x: groupAccessArea.x2, y: groupAccessArea.y1 }) // 最小区域 四角 matrixPoints.push({ x: groupForbiddenArea.x1, y: groupForbiddenArea.y1 }) matrixPoints.push({ x: groupForbiddenArea.x2, y: groupForbiddenArea.y2 }) matrixPoints.push({ x: groupForbiddenArea.x1, y: groupForbiddenArea.y2 }) matrixPoints.push({ x: groupForbiddenArea.x2, y: groupForbiddenArea.y1 }) // 起点 matrixPoints.push({ ...fromAnchorPos, type: 'from' }) // 起点 出口 matrixPoints.push({ ...fromEntry, type: 'from-entry' }) // 终点 matrixPoints.push({ ...toAnchorPos, type: 'to' }) // 终点 入口 matrixPoints.push({ ...toEntry, type: 'to-entry' }) // 通过区域 中点 matrixPoints.push({ x: (groupAccessArea.x1 + groupAccessArea.x2) * 0.5, y: (groupAccessArea.y1 + groupAccessArea.y2) * 0.5 }) // 去重 matrixPoints = matrixPoints.reduce( (arr, item) => { if (item.type === void 0) { if (arr.findIndex((o) => o.x === item.x && o.y === item.y) < 0) { arr.push(item) } } else { const idx = arr.findIndex((o) => o.x === item.x && o.y === item.y) if (idx > -1) { arr.splice(idx, 1) } arr.push(item) } return arr }, [] as typeof matrixPoints ) // 上文提到的:“墙”不同于连接点,需要补充一些点 const columns = [ ...matrixPoints.map((o) => o.x), // 增加列 fromGroupForbiddenArea.x1, fromGroupForbiddenArea.x2, toGroupForbiddenArea.x1, toGroupForbiddenArea.x2 ].sort((a, b) => a - b) // 去重 for (let x = columns.length - 1; x > 0; x--) { if (columns[x] === columns[x - 1]) { columns.splice(x, 1) } } const rows = [ ...matrixPoints.map((o) => o.y), // 增加行 fromGroupForbiddenArea.y1, fromGroupForbiddenArea.y2, toGroupForbiddenArea.y1, toGroupForbiddenArea.y2 ].sort((a, b) => a - b) // 去重 for (let y = rows.length - 1; y > 0; y--) { if (rows[y] === rows[y - 1]) { rows.splice(y, 1) } } // 屏蔽区域(序号) const columnFromStart = columns.findIndex((o) => o === fromGroupForbiddenArea.x1) const columnFromEnd = columns.findIndex((o) => o === fromGroupForbiddenArea.x2) const rowFromStart = rows.findIndex((o) => o === fromGroupForbiddenArea.y1) const rowFromEnd = rows.findIndex((o) => o === fromGroupForbiddenArea.y2) const columnToStart = columns.findIndex((o) => o === toGroupForbiddenArea.x1) const columnToEnd = columns.findIndex((o) => o === toGroupForbiddenArea.x2) const rowToStart = rows.findIndex((o) => o === toGroupForbiddenArea.y1) const rowToEnd = rows.findIndex((o) => o === toGroupForbiddenArea.y2) // 算法矩阵起点、终点 let matrixStart: Konva.Vector2d | null = null let matrixEnd: Konva.Vector2d | null = null // 算法地图矩阵 const matrix: Array<number[]> = [] for (let y = 0; y < rows.length; y++) { // 新增行 if (matrix[y] === void 0) { matrix[y] = [] } for (let x = 0; x < columns.length; x++) { // 不可通过区域(把范围内的点设定为“墙”) if ( x >= columnFromStart && x <= columnFromEnd && y >= rowFromStart && y <= rowFromEnd ) { // 起点节点范围内 matrix[y][x] = 2 } else if ( x >= columnToStart && x <= columnToEnd && y >= rowToStart && y <= rowToEnd ) { // 终点节点范围内 matrix[y][x] = 2 } else { // 可通过区域 matrix[y][x] = 0 } // 起点、终点 -> 算法 起点、终点 if (columns[x] === fromAnchorPos.x && rows[y] === fromAnchorPos.y) { matrixStart = { x, y } } else if (columns[x] === toAnchorPos.x && rows[y] === toAnchorPos.y) { matrixEnd = { x, y } } // 从 不可通过区域 中找 起点、出口、终点、入口,设置为 可通过(因为与不可通过区域有重叠,所以要单独设置一下) if (fromEntry.x === fromAnchorPos.x) { if ( columns[x] === fromAnchorPos.x && rows[y] >= Math.min(fromEntry.y, fromAnchorPos.y) && rows[y] <= Math.max(fromEntry.y, fromAnchorPos.y) ) { matrix[y][x] = 1 } } else if (fromEntry.y === fromAnchorPos.y) { if ( columns[x] >= Math.min(fromEntry.x, fromAnchorPos.x) && columns[x] <= Math.max(fromEntry.x, fromAnchorPos.x) && rows[y] === fromAnchorPos.y ) { matrix[y][x] = 1 } } if (toEntry.x === toAnchorPos.x) { if ( columns[x] === toAnchorPos.x && rows[y] >= Math.min(toEntry.y, toAnchorPos.y) && rows[y] <= Math.max(toEntry.y, toAnchorPos.y) ) { matrix[y][x] = 1 } } else if (toEntry.y === toAnchorPos.y) { if ( columns[x] >= Math.min(toEntry.x, toAnchorPos.x) && columns[x] <= Math.max(toEntry.x, toAnchorPos.x) && rows[y] === toAnchorPos.y ) { matrix[y][x] = 1 } } } } if (matrixStart && matrixEnd) { // 算法使用 const way = aStar({ from: matrixStart, to: matrixEnd, matrix, maxCost: 2 }) // 画线 this.group.add( new Konva.Line({ name: 'link-line', // 用于删除连接线 groupId: fromGroup.id(), pointId: fromPoint.id, pairId: pair.id, // points: _.flatten( way.map((o) => [ this.render.toStageValue(columns[o.x]), this.render.toStageValue(rows[o.y]) ]) ), stroke: 'red', strokeWidth: 2 }) ) } } } } // 略 }
关于代码里提到的“动态缩短连接点及其出入口的距离”,上面代码里的“groupDistance”变量,由于我们人为定义了连接点的出入口,出入口距离连接点是存在一些距离的,当两个节点距离太近的时候,其实就是两个出入口在某一方向上挨在一起,导致算法认为“无路可走”,无法绘制连接线了:
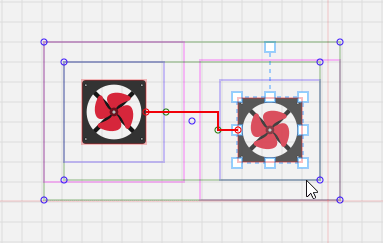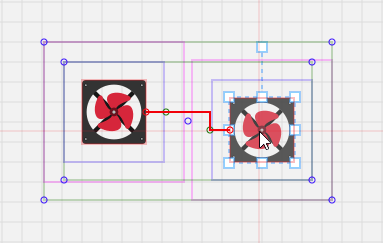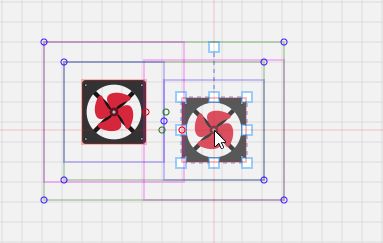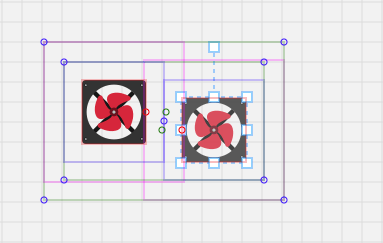
因此,当两个节点距离太近的时候,动态缩小这个距离:
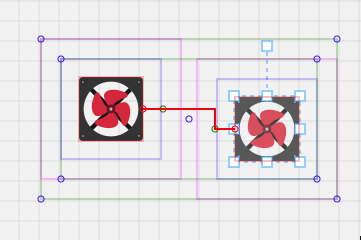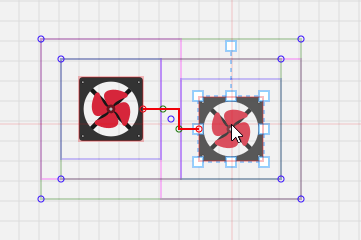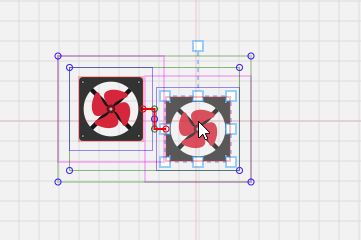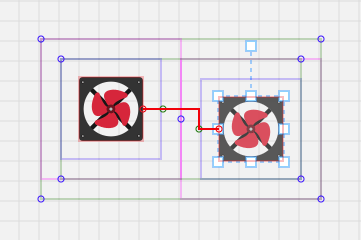
这里定义了,动态的距离范围在 6px ~ 背景网格大小 之间,取决于两个节点之间的最短距离。
getGroupPairDistance(groupArea1: Area, groupArea2: Area): number { const xs = [groupArea1.x1, groupArea1.x2, groupArea2.x1, groupArea2.x2] const maxX = Math.max(...xs) const minX = Math.min(...xs) const dx = maxX - minX - (groupArea1.x2 - groupArea1.x1 + (groupArea2.x2 - groupArea2.x1)) const ys = [groupArea1.y1, groupArea1.y2, groupArea2.y1, groupArea2.y2] const maxY = Math.max(...ys) const minY = Math.min(...ys) const dy = maxY - minY - (groupArea1.y2 - groupArea1.y1 + (groupArea2.y2 - groupArea2.y1)) // return this.render.toBoardValue( Math.min(this.render.bgSize, Math.max(dx < 6 ? 6 : dx, dy < 6 ? 6 : dy) * 0.5) ) }
另外,代码里计算 不可通过区域 的“groupDistance - 2”,减去2个像素点原因是,人为与外层区域留了点空隙,距离缩小至动态范围内,两节点总有空间用于计算数据模型。
下面,逐个说明一下工具方法:
其实就是,所有锚点占用的最小矩形区域
// 元素(连接点们)最小区域(绝对值) getGroupLinkArea(group?: Konva.Group): Area { let area: Area = { x1: 0, y1: 0, x2: 0, y2: 0 } if (group) { // stage 状态 const stageState = this.render.getStageState() const anchors = group.find('.link-anchor') const positions = anchors.map((o) => o.absolutePosition()) area = { x1: Math.min(...positions.map((o) => o.x)) - stageState.x, y1: Math.min(...positions.map((o) => o.y)) - stageState.y, x2: Math.max(...positions.map((o) => o.x)) - stageState.x, y2: Math.max(...positions.map((o) => o.y)) - stageState.y } } return area }
其实就是在传入区域基础上,增加内边距(目前 gap 也就是 groupDistance):
// 连线不可通过区域 getGroupForbiddenArea(groupArea: Area, gap: number): Area { const area: Area = { x1: groupArea.x1 - gap, y1: groupArea.y1 - gap, x2: groupArea.x2 + gap, y2: groupArea.y2 + gap } return area }
同上
// 连线通过区域 getGroupAccessArea(groupArea: Area, gap: number): Area { const area: Area = { x1: groupArea.x1 - gap, y1: groupArea.y1 - gap, x2: groupArea.x2 + gap, y2: groupArea.y2 + gap } return area }
两个区域占用的最小矩形区域
// 两区域扩展 getGroupPairArea(groupArea1: Area, groupArea2: Area): Area { const area: Area = { x1: Math.min(groupArea1.x1, groupArea2.x1), y1: Math.min(groupArea1.y1, groupArea2.y1), x2: Math.max(groupArea1.x2, groupArea2.x2), y2: Math.max(groupArea1.y2, groupArea2.y2) } return area }
通过元素最小区域和锚点,得出该锚点的出入口
// 连接出入口 getEntry(anchor: Konva.Node, groupLinkArea: Area, gap: number): Konva.Vector2d { // stage 状态 const stageState = this.render.getStageState() let entry: Konva.Vector2d = { x: 0, y: 0 } const fromPos = anchor.absolutePosition() if (fromPos.x - stageState.x === groupLinkArea.x1) { entry = { x: fromPos.x - gap - stageState.x, y: fromPos.y - stageState.y } } else if (fromPos.x - stageState.x === groupLinkArea.x2) { entry = { x: fromPos.x + gap - stageState.x, y: fromPos.y - stageState.y } } else if (fromPos.y - stageState.y === groupLinkArea.y1) { entry = { x: fromPos.x - stageState.x, y: fromPos.y - gap - stageState.y } } else if (fromPos.y - stageState.y === groupLinkArea.y2) { entry = { x: fromPos.x - stageState.x, y: fromPos.y + gap - stageState.y } } return entry }
到此,折线绘制的主要逻辑就完成了。
已知缺陷
从 Issue 中得知,当节点进行说 transform rotate 旋转的时候,对齐就会出问题。相应的,绘制连接线(折线)的场景也有类似的问题,大家多多支持,后面抽空研究处理一下(-_-)。。。
More Stars please!勾勾手指~
源码
gitee源码
示例地址